
2006年广东韶关市高中阶段学校招生考试(大纲卷)
一、选择题(本题共10小题,每小题3分,共30分,每小题给出4个答案,其中只有一个正确)
1.点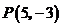 关于原点对称的点的坐标是( )
关于原点对称的点的坐标是( )
A.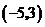 B.
B.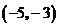 C.
C.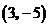 D.
D.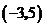
2.据统计,今年“五 一”黄金周来韶关旅游的游客人数为
一”黄金周来韶关旅游的游客人数为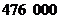 人.用科学记数法表示游客人数,正确的是( )
人.用科学记数法表示游客人数,正确的是( )
A.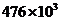 B.
B.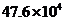 C.
C.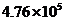 D.
D.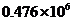
3.下列计算正确的是( )
A.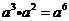 B.
B.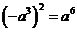 C.
C.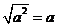 D.
D.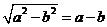
 4.已知函数
4.已知函数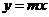 与
与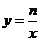 在同一直角坐标系中的图象大致如图,则下列结论正确的是( )
在同一直角坐标系中的图象大致如图,则下列结论正确的是( )
A.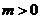 ,
, B.
B.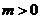 ,
,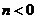
C. ,
, D.
D. ,
,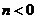
5.已知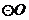 的半径为
的半径为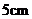 ,如果圆心
,如果圆心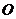 到直线
到直线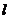 的距离为
的距离为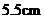 ,那么直线
,那么直线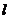 和
和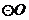 的位置关系是( )
的位置关系是( )
A.相交 B.相切 C.相离 D.相交或相离
6.设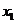 ,
,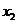 是方程
是方程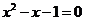 的两根,则
的两根,则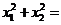 ( )
( )
A.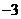 B.
B.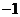 C.
C.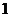 D.
D.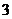
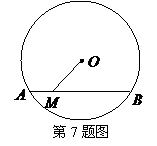
7.如右图,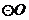 的半径为
的半径为 ,弦
,弦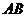 的长为
的长为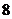 ,
,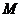 是弦
是弦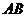 上的动点,则线段
上的动点,则线段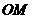 长的最小值为( )
长的最小值为( )
 A.
A. B.
B.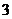 C.
C.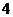 D.
D.
8.已知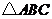 中,
中,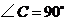 ,
,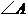 ,
,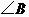 ,
,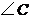 所对的边分别是
所对的边分别是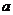 ,
,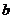 ,
,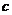 ,且
,且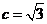 ,
,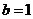 ,则
,则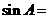 ( )
( )
A. B.
B.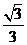 C.
C.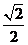 D.
D.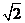
9.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
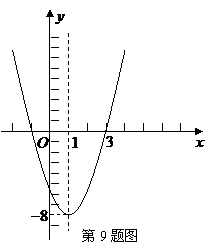 A.
A.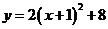 B.
B.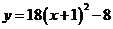
C. D.
D.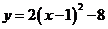
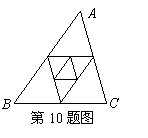 10.如右图,已知
10.如右图,已知 的周长为
的周长为 ,连结
,连结 三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,
三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形, ,依此类推,则第10个三角形的周长为( )
,依此类推,则第10个三角形的周长为( )
A.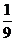 B.
B.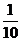 C.
C.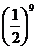 D.
D.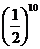
二、填空题(本题共5小题,每小题3分,共15分)
11.计算: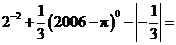 __________.
__________.
12.对甲、乙两台机床生产的同一种型号的零件进行抽样检测(零件个数相同),其平均数、方差的计算结果是:机床甲: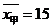 ,
,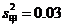 ;机床乙:
;机床乙: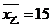 ,
,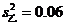 .由此可知:__________(填甲或乙)机床性能较好.
.由此可知:__________(填甲或乙)机床性能较好.
13.用换元法解方程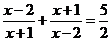 ,如果设
,如果设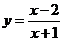 ,那么原方程化为关于
,那么原方程化为关于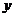 的整式方程是__________.
的整式方程是__________.
14.如右图,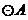 ,
,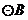 ,
, ,
,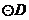 相互外离,它们的半径都是
相互外离,它们的半径都是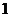 ,顺次连结四个圆心得到四边形
,顺次连结四个圆心得到四边形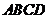 ,则图中四个扇形(阴影部分)的面积之和等于__________.(结果保留
,则图中四个扇形(阴影部分)的面积之和等于__________.(结果保留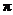 )
)
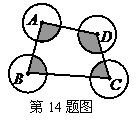 |
15.当 __________时,关于
__________时,关于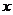 的方程
的方程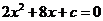 有实数根.(填一个符合要求的数即可)
有实数根.(填一个符合要求的数即可)
三、解答题(本大题共5小题,其中第16,17小题各6分,第18,19,20小题各7分,共33分)
16.先化简,再求值: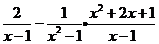 ,其中
,其中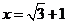 .
.
 17.解不等式组
17.解不等式组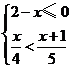 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
 18.尺规作图:已知直线
18.尺规作图:已知直线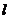 和
和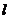 外一点
外一点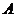 ,求作
,求作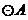 ,使
,使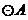 与直线
与直线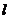 相切.(保留作图痕迹,不必写作法和证明)
相切.(保留作图痕迹,不必写作法和证明)
(1)求第三小组的频率,并补全这个频率分布直方图;
(2)参赛学生成绩的中位数落在第几小组内?
19.希望中学在今年的校园科技文化节中举行了初三年级数学竞赛,李老师将参赛学生的成绩(得分均为整数,满分为100分)进行整理后分成五组,绘制了右边的频率分布直方图,已知图中从左到右的第一、第二、第四、第五小组的频率分别是 ,
, ,
, ,
, ,第三小组的频数为
,第三小组的频数为 .请你帮助李老师完成下列问题:
.请你帮助李老师完成下列问题:
 (3)若成绩在80分以上(不含80分)的学生就能获得一等奖,求这次比赛中获得一等奖的学生人数.
(3)若成绩在80分以上(不含80分)的学生就能获得一等奖,求这次比赛中获得一等奖的学生人数.
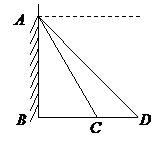 20.如图,某人从楼顶
20.如图,某人从楼顶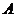 看地面
看地面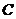 ,
,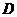 两点,测得它们的俯角分别是
两点,测得它们的俯角分别是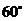 和
和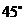 .已知
.已知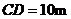 ,
,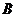 ,
,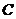 ,
,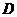 在同一直线上,求楼高
在同一直线上,求楼高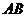 .
.
(精确到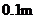 ,参考数据:
,参考数据: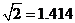 ,
,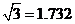 )
)
四、解答题(本大题共3小题,每小题8分,共24分)
21.已知某种型号的摩托车油箱中的剩余油量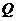 (升)是它行驶的时间
(升)是它行驶的时间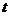 (小时)的一次函数.某天老李骑该种摩托车外出旅游,刚开始行驶时,油箱中有油
(小时)的一次函数.某天老李骑该种摩托车外出旅游,刚开始行驶时,油箱中有油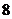 升,行驶了
升,行驶了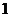 小时后,他发现已耗油
小时后,他发现已耗油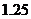 升.
升.
(1)求油箱中的剩余油量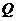 (升)与行驶的时间
(升)与行驶的时间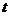 (小时)的函数关系式,并求出自变量
(小时)的函数关系式,并求出自变量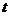 的取值范围;
的取值范围;
(2)在给定的直角坐标系中画出此函数的图象;
 (3)从开始行驶算起,如果摩托车以每小时50千米的速度匀速行驶,当油箱中的剩余油量为
(3)从开始行驶算起,如果摩托车以每小时50千米的速度匀速行驶,当油箱中的剩余油量为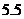 升时,该摩托车行驶了多少千米?
升时,该摩托车行驶了多少千米?
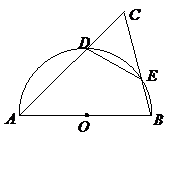 22.如图,在
22.如图,在 中,
中,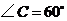 ,以
,以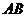 为直径的半圆
为直径的半圆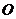 分别交
分别交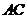 ,
,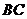 于点
于点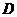 ,
,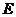 ,已知
,已知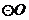 的半径为
的半径为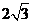 .
.
(1)求证: ;
;
(2)求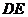 的长.
的长.
23.某商店从厂家以每件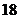 元的价格购进一批商品,该商店可以自行定价.据市场调查,该商品的售价与销售量的关系是:若每件售价
元的价格购进一批商品,该商店可以自行定价.据市场调查,该商品的售价与销售量的关系是:若每件售价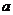 元,则可卖出
元,则可卖出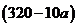 件,但物价部门限定每件商品加价不能超过进货价的
件,但物价部门限定每件商品加价不能超过进货价的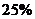 .如果商店计划要获利400元,则每件商品的售价应定为多少元?需要卖出这种商品多少件?(每件商品的利润=售价
.如果商店计划要获利400元,则每件商品的售价应定为多少元?需要卖出这种商品多少件?(每件商品的利润=售价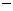 进货价)
进货价)
五、解答题(本大题共2小题,每小题9分,共18分)
24.如图,在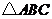 中,
中, ,
,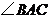 的外角平分线交直线
的外角平分线交直线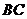 于
于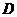 ,过
,过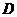 作
作 ,
,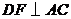 分别交直线
分别交直线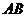 ,
,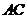 于
于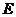 ,
, ,连结
,连结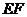 .
.
 (1)求证:
(1)求证: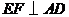 ;
;
(2)若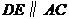 ,且
,且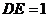 ,求
,求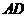 的长.
的长.
25.如图,在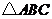 中,
中,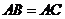 ,
,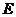 是高
是高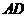 上的动点,
上的动点, 是点
是点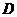 关于点
关于点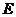 的对称点(点
的对称点(点 在高
在高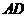 上,且不与
上,且不与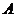 ,
,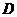 重合).过点
重合).过点 作
作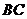 的平行线与
的平行线与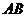 交于
交于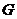 ,与
,与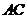 交于
交于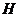 ,连结
,连结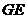 并延长交
并延长交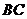 于点
于点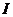 ,连结
,连结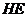 并延长交
并延长交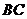 于点
于点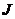 ,连结
,连结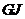 ,
,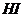 .
.
(1)求证:四边形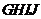 是矩形;
是矩形;
(2)若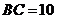 ,
, ,设
,设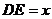 ,
, .
.
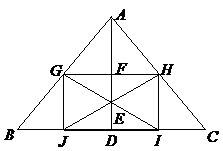 ①求
①求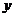 与
与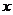 的函数关系式,并写出自变量
的函数关系式,并写出自变量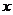 的取值范围;
的取值范围;
②点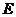 在何处时,矩形
在何处时,矩形 的面积与
的面积与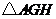 的面积相等?
的面积相等?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com