第9题图 从2002年到2006年,这两家公司中销售量增长较快的是 .
试题详情
10.化简: = . = . 试题详情
11.某市在旧城改造过程中,需要整修一段全长2400m的道路.为了尽量减少施工对城市交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8小时完成任务.求原计划每小时修路的长度.若设原计划每小时修路x m,则根据题意可得方程
. 试题详情
12.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为 cm. 试题详情

第12题图
第13题图 试题详情
13.如图,△ABC的顶点坐标分别为A ( 3,6 ),B ( 1,3 ),C ( 4,2 ) .如果将△ABC绕C点顺时针旋转90 º,得到△A′B′C′,那么点A的对应点A′ 的坐标为(
). 试题详情
14.一个大长方体是由四个完全一样的小长方体拼成的,如果每个小长方体的长、宽、高分别是3、1、1,那么这个大长方体的表面积可能有
种不同的值,其中最小值为
. 用圆规、直尺作图,不写作法,但要保留作图痕迹. 试题详情
三、作图题(本题满分6分) 15.青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C 的距离相等. 试题详情
 (1)若三所运动员公寓A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置; (1)若三所运动员公寓A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置;
(2)若∠BAC=66º,则∠BPC=
º. 试题详情
四、解答题(本题满分72分,共有9道小题) 16.(本小题满分6分)解方程组: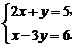 试题详情
17.(本小题满分6分) 某学校为了解该校七年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm): 试题详情

(1)请根据所提供的信息补全频数分布直方图; (2)样本的中位数在统计图的哪个范围内? 试题详情
(3)如果上述样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么_________(填“七年级”或“八年级”)学生的身高比较整齐. 试题详情
试题详情
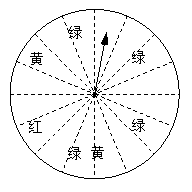 在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的 在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的
转盘(如图,转盘被平均分成16份),并规定:顾客每购买100元的商品, 就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄 色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券, 凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接 获得购物券10元. (1)求每转动一次转盘所获购物券金额的平均数; (2)如果你在该商场消费125元,你会选择转转盘还是直接获得购物券?说明理由. 试题详情
试题详情
一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北63.5°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近? 试题详情
试题详情
试题详情
20.(本小题满分8分) 某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解答下列问题: (1)有几种符合题意的生产方案?写出解答过程; 试题详情
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低? 原料名称 饮料名称 甲 乙 A 20克 40克 B 30克 20克 试题详情
21.(本小题满分8分) 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF. (1)求证:△ABE≌△AD′F; 试题详情
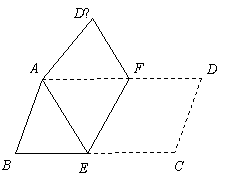 (2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论. (2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
试题详情
试题详情
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:w=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题: (1)求y与x的关系式; (2)当x取何值时,y的值最大? (3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元? 试题详情
23.(本小题满分10分) 提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系? 探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手: 试题详情
 (1)当AP= (1)当AP=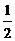 AD时(如图②): AD时(如图②):
试题详情
∵AP=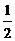 AD,△ABP和△ABD的高相等, AD,△ABP和△ABD的高相等, 试题详情
∴S△ABP=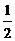 S△ABD . S△ABD . 试题详情
∵PD=AD-AP=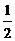 AD,△CDP和△CDA的高相等, AD,△CDP和△CDA的高相等, 试题详情
 ∴S△CDP= ∴S△CDP=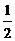 S△CDA . S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP 试题详情
=S四边形ABCD-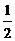 S△ABD- S△ABD-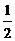 S△CDA S△CDA 试题详情
=S四边形ABCD-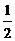 (S四边形ABCD-S△DBC)- (S四边形ABCD-S△DBC)-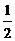 (S四边形ABCD-S△ABC) (S四边形ABCD-S△ABC) 试题详情
=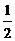 S△DBC+ S△DBC+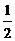 S△ABC . S△ABC . 试题详情
(2)当AP= AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程; AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程; 试题详情
(3)当AP= AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________________; AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________________; 试题详情
(4)一般地,当AP= AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程; AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程; 试题详情
问题解决:当AP=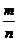 AD(0≤ AD(0≤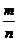 ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________. ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________. 试题详情
试题详情
 已知:如图,△ABC是边长3cm的等边三角形,动点 已知:如图,△ABC是边长3cm的等边三角形,动点
P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移 动,它们的速度都是1cm/s,当点P到达点B时,P、Q两 点停止运动.设点P的运动时间为t(s),解答下列问题: (1)当t为何值时,△PBQ是直角三角形? (2)设四边形APQC的面积为y(cm2),求y与t的 关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出相应的t值;不存在,说明理由; (3)设PQ的长为x(cm),试确定y与x之间的关系式. 试题详情
试题详情
| 
 (考试时间:120分钟;满分:120分)
(考试时间:120分钟;满分:120分) 的绝对值等于( ).
的绝对值等于( ). B.
B. D.
D.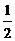





 B.
B. C.
C.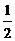 D.
D.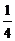
 B.
B.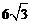 D.12
D.12
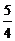 m3 B.小于
m3 B.小于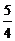 m
m m3 D.小于
m3 D.小于 m3
m3 = .
= .