
西安市第一中学
2007―2008学年度第二学期第五次模拟考试题
高三数学(理)
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1、设集合 若
若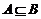 ,则
,则 的范围是( ).
的范围是( ).
(A) (B)
(B) (C)
(C) (D)
(D)
2、 的值为( ).
的值为( ).
(A) 0
(B) 1
(C) 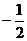 (D)
(D)
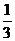
3、复数 ( ).
( ).
(A)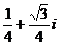 (B)
(B) (C)
(C) (D)
(D)
4、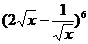 的展开式中含
的展开式中含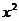 项的系数是(
).
项的系数是(
).
(A)240
(B)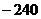 (C)192 (
D)
(C)192 (
D)
5、已知函数 的图像与函数
的图像与函数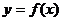 的图像关于直线
的图像关于直线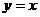 对称,则( ).
对称,则( ).
(A)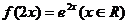 (B)
(B)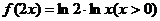
(C) 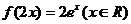 (D)
(D)
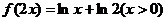
6、一个长方体共一顶点的三个面的面积分别是 ,这个长方体的体对角线的长是( ).
,这个长方体的体对角线的长是( ).
(A) (B)
(B)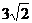 (C)
(C) (D)
(D)
7、已知双曲线 的一条准线与抛物线
的一条准线与抛物线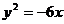 的准线重合,则该双曲线的离心率为( ).
的准线重合,则该双曲线的离心率为( ).






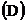
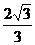
8、函数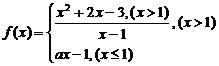 在
在 处连续,则a的值为( ).
处连续,则a的值为( ).
(A)5 (B)3 (C)2 (D)1
9、从0,1,2,3,4,5,6,7,8,9十个数字中,选出一个偶数和三个奇数,组成一个没有重复数字的四位数,这样的四位数共有( ).
(A)1440个 (B)1480个 (C)1140个 (D)1200个
10、已知平面上直线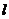 的方向向量
的方向向量 ,点
,点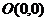 和
和 在
在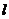 上的射影分别是
上的射影分别是 和
和 ,则
,则 ,其中
,其中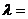 ( ).
( ).
(A) (B)
(B)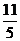 (C)
(C) (D)
(D)
11、函数 上的点到直线
上的点到直线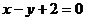 的距离的最小值是( ).
的距离的最小值是( ).
(A)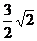 (B)
(B) (C)
(C)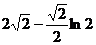 (D)
(D)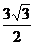
12、一个四面体ABCD的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( ) .
,四个顶点在同一球面上,则此球的表面积为( ) .
(A) (B)
(B) (C)
(C) (D)
(D)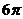
二、填空题:(本大题共4个小题,每小题4分,共16分.把答案填在题中答题卷横线上).
13、已知 中,点
中,点 的坐标分别为
的坐标分别为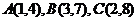 则
则 的面积为 .
的面积为 .
14、不等式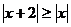 的解集是 .
的解集是 .
15、已知符号函数 ,则不等式
,则不等式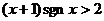 的解集是
.
的解集是
.
16、已知数列{an}中,a1=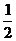 ,an=an-1+
,an=an-1+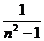 (n≥2),则数列{an}的通项公式为______.
(n≥2),则数列{an}的通项公式为______.
三、解答题:(本大题共6个小题,共74分.解答应写出文字说明,证明过程或演算步骤).
17、(本小题满分12分)
设 分别为
分别为 ㄓABC的边BC、CA、AB的长,且
ㄓABC的边BC、CA、AB的长,且 (
(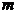 为常数).若
为常数).若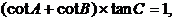 求
求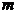 的值.
的值.
18、(本小题满分12分)
某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是相互独立的,并且胜场的概率是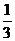 .
.
(1)求这支篮球队首次胜场前已负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望与方差.
19、(本小题满分12分)
设数列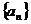 的前
的前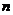 项和为
项和为 ,若对所有的非零自然数
,若对所有的非零自然数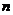 ,都有
,都有
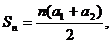 求证:
求证: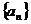 为等差数列.
为等差数列.
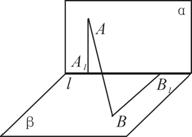 20.(本题?分12分)
20.(本题?分12分)
如图1, ,点
,点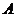 在
在
直线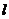 上的射影为
上的射影为 ,点
,点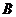 在直线
在直线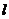 上的射影为
上的射影为
已知 ,
,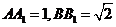 ,求:
,求:
(1)直线 分别与平面
分别与平面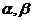 所成角的大小;
图1
所成角的大小;
图1
(2)二面角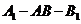 的大小.
的大小.
21、(本小题满分12分)
已知长度为 的线段
的线段 的两端点在抛物线
的两端点在抛物线 上移动,求线段
上移动,求线段 的中点
的中点 的轨迹方程.
的轨迹方程.
22、(本小题满分14分)
由原点 向三次曲线
向三次曲线 引切线,切于不同于点
引切线,切于不同于点 的点
的点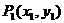 ,再由点
,再由点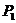 引此曲线的切线,切于不同于点
引此曲线的切线,切于不同于点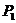 的点
的点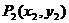 ,如此继续作下去,直到得到点列
,如此继续作下去,直到得到点列 ,试回答下列问题:
,试回答下列问题:
(1)求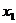 ;
;
(2)求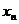 与
与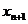 的关系;
的关系;
(3)若 ,求证:当n为正偶数时,
,求证:当n为正偶数时, ;当
;当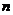 为正奇数时,
为正奇数时,  .
.
西安市第一中学
2007―2008学年度第二学期第五次模拟考试
一.选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
D
D
B
D
A
C
C
A
A
二.填空题(每小题4分,共16分)
13.  14.
14.  15.
15.  16.
16. 
 -
-
三、解答题:(本大题共6个小题,共74分.解答应写出文字说明,证明过程或演算步骤).
17、(本小题满分12分)
解:由 得:
得:
 (3分)
(3分)
因为 所以
所以 所以
所以 (6分)
(6分)
由正弦定理得 . (8分) 从而由余弦定理及
. (8分) 从而由余弦定理及 得:
得:

 (12分)
(12分)
18、(本小题满分12分)
解:(1)∵这支篮球队与其他各队比赛胜场的事件是相互独立的,
∴首次胜场前已负了两场的概率P=(1- )×(1-
)×(1- )×
)× =
= . 4分
. 4分
(2)设A表示这支篮球队在6场比赛中恰好胜了3场的事件,则P(A)就是6次独立重复试验中恰好发生3次的概率.∴P(A)=P6(3)=C (
( )3(1-
)3(1- )3=
)3= .
8分
.
8分
(3)设ξ表示这支篮球队在6场比赛中胜场数,则ξ~B(6, ).
).
∴Dξ=6× ×(1-
×(1- )=
)= ,Eξ=6×
,Eξ=6× =2.
=2.
故这支篮球队在6场比赛中胜场数的期望是2,方差是 .
12分
.
12分
19、(本小题满分12分)
解: 
 (4分)
(4分)
 ,
,
 ( 6分)
( 6分)
当 时,
时, 当
当 时,
时, ,(9分)
,(9分)
 当
当 时,
时,
当 时,
时, (11分)
(11分)
综上, 

 所以,
所以, 为等差数列.(12分)
为等差数列.(12分)
20.(本题?分12分)
解 (1)如图2,将已知条件实现在长方体中,则直线 与平面
与平面 所成的角为
所成的角为 ,ks5u直线
,ks5u直线 与平面
与平面 所成角的为
所成角的为 .在直角
.在直角 中,有
中,有 ,故
,故 =
= ;在直角
;在直角 中,有
中,有 ,
,
故 =
= . 6分
. 6分
(2)如图2,作 有
有

设二面角 的平面角为
的平面角为 ,则
,则


得: .
12分
.
12分
21、(本小题满分12分)
解:因为线段 的两端点在抛物线
的两端点在抛物线 上,故可设
上,故可设 ,设线段
,设线段 的中点
的中点 ,则
,则 7分
7分
又 ,
,
所以: 11分
11分
所以,线段 的中点
的中点 的轨迹方程为
的轨迹方程为 . 12分
. 12分
22、(本小题满分14分)
(1)解:f′(x)=3x2-6ax+b,
过P1(x1,y1)的切线方程是y-y1=f′(x1)(x-x1)(x1≠0).
又原点在直线上,所以-(x13-3ax12+bx1)=(-x1)(3x12-6ax1+b),
解得x1= . 4分
. 4分
(2)解:过Pn(xn,yn)的切线方程是y-yn=f′(xn)(x-xn).
又Pn+1 (xn+1,yn+1)在直线上,
所以(xn+1-xn)2(xn+1+2xn-
解得xn+1+2xn-
(3)证明:由(2)得xn+1-a=-2(xn-a),
所以数列{xn-a}是首项为x1-a= ,公比为-2的等比数列.
,公比为-2的等比数列.
∴xn=a+ ?(-2)n-1,
?(-2)n-1,
即xn=[1-(-2)n-2]a.
当n为正偶数时,xn<a;当n为正奇数时, xn>a. 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com