1．小华来到一家有2层楼座的大型影院，买了票后，如果他想知道自己的具体位置，那需从电影票上找到相关数据（    ）

A．1个          B．2个          C．3个        D．4个

2．点P（-2，1）关于x轴的对称点的坐标为（    ）

A．（2，1）      B．（-2，-1）      C．（2，-1）    D．（1，-2）

3．已知点P（a，b）是平面直角坐标系中第二象限的点，则化简?a―b?+?b―a?的结果是（    ）

A．-2a+2b        B．2a            C．2a―2b      D．0

4．在平面直角坐标系中，有一点P（a，b），若ab=0，，由点P一定在（    ）

A．x轴上        B．y轴上        C．原点         D．坐标轴上

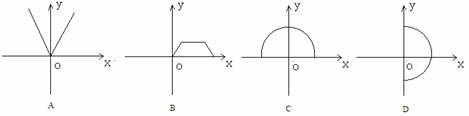
5．下列四个图象中，不表示某一函数图象的是（    ）

6．若一次函数y=2x-b的图象不经过第二象限，则（    ）

A．b＞0         B．b＜0           C．b≥0         D．b≤0

7．若（-5，y₁），（-3，y₂）是一次函数y=-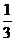x+2图象上的两点，则y₁与y₂的大小关系是（    ）

A．y₁＞y₂            B．y₁＜y₂              C．y₁=y₂             D．无法比较

8．在密码学中，直接可以看到的内容为明码，对明码进行某种处理后得到的内容为密码．有一种密码，将英文26个字母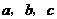，…，（不论大小写）依次对应1，2，3，…，26这26个自然数（见表格）．当明码对应的序号为奇数时，密码对应的序号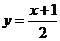；当明码对应的序号为偶数时，密码对应的序号．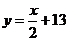

字母

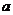
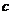
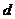
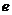
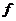
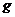
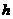
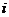
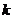
序号

1

2

3

4

5

6

7

8

9

10

11

12

13

字母

序号

14

15

16

17

18

19

20

21

22

23

24

25

26

按上述规定，将明码“love”译成密码是（    ）

A．gawq        B．shxc         C．sdri          D．love

9．如图，小亮在操场上玩，能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是（    ）

10．如图，一次函数经过点A与正比例函数y=-x的图象交于点B，则该一次函数的表达式为（    ）

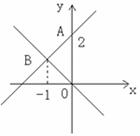
A．y = -x +2            B．y = x+2        C．y = x―2            D．y = -x―2           

11．图中表示一次函数y₁=mx+n与正比例函数y₂=mnx (m、n是常数，且mn≠0)图象的是（    ）

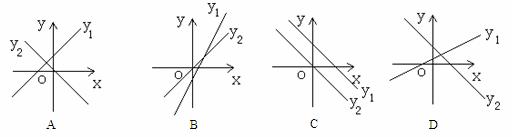
12．某水电站的蓄水池有2个进水口，一个出水口，每个进水口进水量与时间的关系如

图甲所示，出水口出水量与时间关系如图乙所示，已知某天0点到6点进行机组试运行，试机时至少打开一个水口，且该水池的蓄水量与时间的关系如图丙所示，给出以下3个判断：

①0点到3点，只进水不出水  ②3点到4点，不进水只出水  ③4点到6点，不进水不出水，则上述判断中，一定正确的有（    ）个

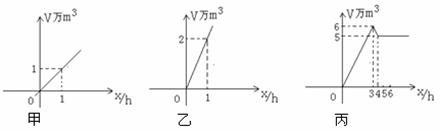
A．0个          B．1个         C．2个       D．3个

13．已知，点P在第四象限，且到x轴的距离为2，到y轴的距离为3，则点P的坐标为       。

14．已知，点A（0，0）、B（3，0），点C在y轴上，且△ABC的面积是5，则点C的坐标为              。

15．点A（4，y）和B（x，-3），过A、B的直线平行于x轴，且AB=5，则x+y=   

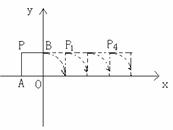
16．如图，将边长为1的正方形OAPB沿x轴正方向连续翻转2005次，点P依次落在P₁、P₂、P₃……P₂₀₀₅的位置，则P₂₀₀₅的坐标是          。

17．一次函数y=(1―3m)x-2m的函数值y随x的增大而增大，且与y轴交于负半轴，则m的取值范围是           。

18．一次函数y=x-5的图象经过点P（a，b）和点Q（c，d），则a（c―d）―b（c―d）的值为           。

19．周长为10cm的等腰三角形，腰长y_(cm)与底边x_(cm)之间的函数关系式为（并写出自变量x的取值范围）                                。

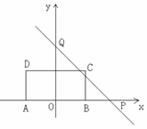
20．如图，矩形ABCD的边AB在x轴上，AB的中点与原点重合，AB=2，AD=1，过定点Q（0，2）和动点P（a，0）的直线与矩形ABCD的边有公共点，则a的取值范围是           。        

21．（本题8分）已知2y―3与3x+1成正比例，且x=2时，y=5

（1）求y与x之间的函数关系式。

（2）当x为何值时，y＞0？

22．（本题8分）下图表示甲骑电动自行车和乙驾驶汽车沿相同的路线行驶45km，由A地到B地时，行驶的路程y（km）与经过的时间x（h）之间的函数关系，请根据这个行驶过程中的图象填空：汽车出发        h与电动自行车相遇；电动自行车的速度为      km/h；汽车的速度为       km/h；汽车比电动自行车早     h到达B地。  

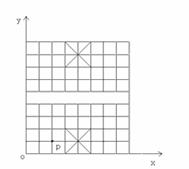
23．（本题8分）平面直角坐标系中，l₁的解析式为y= -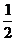x+2，直线l₂的解析式为y= 2x+5

（1）求直线l_l与直线l₂的交点的坐标。

（2）求直线l_l与直线l₂与x轴所围成的图形的面积。

24．（本题10分）如图，我们给中国象棋盘建立一个平面直角坐标系（每个小正方形边长均为1）根据象棋中“马”走“日”的规定，若马的位置在图中的P点

（1）写出下一步“马”可能到达的点的坐标

（2）顺次连接图中的所有点，得到的图形是         

图形（填“中心对称”、“轴对称”）

（3）指出（1）中关于点P成中心对称的点的坐标。

25．（本题10分）如图，直线y= -x+2与x轴、y轴分别交于点A和点B，M是OB上一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，求直线AM的解析式。

26．（本题10分）平行四边形两个顶点的坐标分别为（-3，0）（1，0），第3个顶点在y轴的正半轴上，且与x轴的距离为3个单位长度，求第四个顶点的坐标。

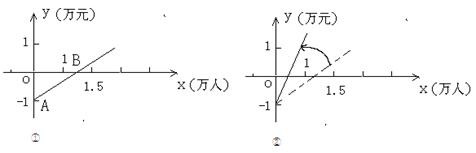
27．(本题12分)如图①是某公共汽车线路收支差额y（票价总收入减去运营成本）与乘客量x的函数图象。目前这条线路亏损，为了扭亏，有关部门举行提高票价的听证会。

乘客代表认为：公交公司应节约能源，改善管理，降低运营成本，以此举实现扭亏。

公交公司认为：运营成本难以下降，公司已尽力，提高票价才能扭亏。

根据这两种意见，可以把图①分别改成图②和图③。

（1）说明图①中点A和点B的实际意义。

（2）你认为图②和图③两个图象中，反映乘客意见的是        ，反映公交公司意见的是          。

（3）如果公交公司采用适当提高票价又减小成本的办法实现扭亏为盈，请你在图④中画出符合这种办法的y与x的大致函数关系图象。

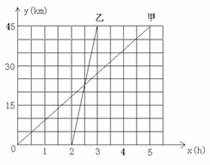
28．（本题12分）甲、乙两名同学进行登山赛，图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中，各自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：

（1）分别求出表示甲、乙两同学登山过程中路程S（km）与时间t（h）的函数关系式（不要求写出自变量t的取值范围）

（2）当甲到达山顶时，乙行进到山路上的某点A处，求A点距山顶的距离

（3）在（2）的条件下，设乙同学从A处继续登山，甲同学到达山顶后休息1h，沿原路下山，在点B处与乙相遇，此时点B与山顶距离为1.5km，相遇后甲、乙各自按原来的路线下山和上山，求乙到达山顶时，甲离山脚的距离是多少千米？

29．（本题12分）一次函数y=kx+k过点（1，4）且分别与x轴，y轴交于A、B两点，

点P（a，0）在x轴正半轴上运动，点Q（0，b）在y轴正半轴上运动，且PQ⊥AB

（1）       求k的值，并画出一次函数的图象

（2）       求a、b满足的等量关系式

（3）       若△APQ是等腰三角形，求△APQ的面积。