1．以直角坐标系的原点O为圆心，以1为半径作圆．若点P是该圆上第一象限内的一点，且OP与x轴正方向组成的角为a，则点P的坐标为    （    ）

A．（cosa，1）    B．（1，sina）    C．（sina，cosa） D．（cosa，sina）

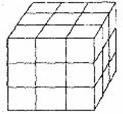
2．如图是由相同小正方体组成的立体图形，则它的左视图为    （    ）

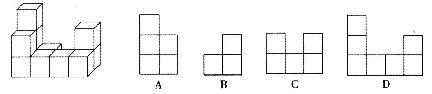
3．已知一1<b<0，0<a<1，那么在代数式a-b，a+b，a+b²，a²-b中，对任意的a，b，对应的代数式的值最大的是    （    ）

    A．a+b       B．a-b               C．a+ b²              D．a²-b

4．现有一列数a₁，a₂，…，a₁₀₀，其中a₃=9，a₇= -7，a₉₈= -1，且满足任意相邻三个数的和为同一个常数．则a₁+a₂+…+a₁₀₀的值为    （    ）

A．0                 B．40                C．32                  D．26

5．下图为某三岔路口交通环岛的简化模型，在某高峰时段，单位时间进出路口A，B，C的机动车辆数如图所示，图中x₁，x₂，x₃分别表示该时段单位时间通过路段弧CA，弧AB，弧BC的机动车辆数（假设：单位时间内，在上述路段中，同一路段上驶入与驶出的车辆数相等），则        （      ）

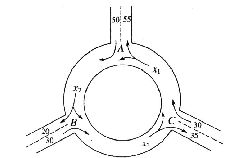
A．x₁> x₂> x₃           B．x₁> x₃> x₂                             C．x₃> x₁> x₂           D．x₃> x₂> x₁

6．将1 m长的绳子，截去一半，然后将剩下的再截去一半，如此下去，若余下的绳子长不足1 cm，则至少需截    （    ）

    A．6次       B．7次                C．8次              D．9次

7．若直线y=3x-1与y=x-k的交点在第四象限，则k的取值范围是    （    ）

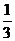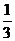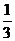A．k<    B．k>1         C．k>1或k<          D．<k<1

8．已知点A，B分别在一次函数y=x，y=8x的图象上，其横坐标分别为a，b（a>0，b>0）．若直线AB为一次函数y=kx+m的图象，则当是整数时，满足条件的整数k的值共有_______个．    （    ）

    A．1                 B．2                   C．3                     D．4

第Ⅱ卷（非选择题共102分）

9．若化简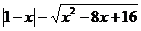的结果为2x-5，则x的取值范围是__________．

10．已知关于x的一元二次方程（1一k）x²-2x -1=0有两个不相等的实数根，则k的最大整数值是__________．

11．如果圆锥的侧面积为20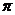cm²，它的母线长为5 cm，那么此圆锥的底面半径等于_____cm．

12．已知样本7，8，9，x，y的平均数是8，标准差是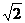，则xy的值为________．

13．如图，将一个体积为27 cm³的正方体木块表面涂上蓝色，然后锯成体积为1 cm³的小正方体，从中任取一块，则这一块恰有两面涂有蓝色的概率是__________．

14．在△ABC中，∠BAC=90⁰，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA。则∠DAE=_________⁰．

15．已知圆C的半径为5，圆内一定点P到圆心C的距离为4，过点P作圆C的弦，则弦长为整数的弦共有_________条．

16．已知不等式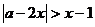，对任意x∈[0，2]恒成立，则a的取值范围是__________

17．已知△ABC的三边的长a，b，c都是正整数，且a≤b≤c，如果b=m（m是正整数），则这样的三角形共有__________个．

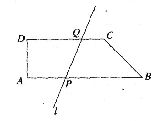
18．如图，在直角梯形ABCD中，∠A为直角，AB∥CD，AB=7，CD=5，AD=2，一条动直线l交AB于点P，交CD于点Q，且将梯形ABCD分成面积相等的两部分，则点A到动直线l的距离的最大值为__________．

19．（本小题满分12分）

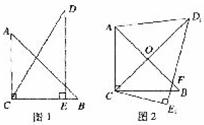
  两个三角形按如图1放置，其中∠ACB=∠DEC=90⁰，∠A=45⁰，∠D=30⁰，且AB=6，DC=7．把△DCE绕点C顺时针旋转15⁰得至△D₁CE₁，如图2，这时AB与CD₁相交于点O，与D₁E₁相交于点F．

（1）求∠ACD₁的度数；

（2）求线段AD₁的长；

（3）若把△D₁CE₁绕点C顺时针再旋转30⁰得到△D₂CE₂这时点B是在△D₂CE₂的内部、外部、还是边上?请说明理由．

20．（本小题满分14分）

某商品期货交易所，2009年5月份交割的贵重金属M，在30天内每张合约的交易价格P（万元）与时间t（天）组成有序数对（t，P），点（t，P）落在两条线段上，每张合约的交易价格P（万元）与时间t（天）的部分数据如下所示：

第t天

1

5

10

15

20

21

25

30

P（万元）

2.2

3

4

5

6

5.9

5.5

5

该贵重金属在30天内（包括30天）的日交易量Q（万张）与时间t（天）的部分数据如下表所示：

第t天

4

10

16

22

Q（万张）

36

30

24

18

（1）根据提供的数据，写出该种贵重金属M每张合约的交易价格P（万元）与时间t（天）所满足的函数关系式；

（2）根据表中数据确定日交易量Q（万张）与时间t（天）的一次函数关系式；

（3）在（2）的结论下，用y（亿元）表示该贵重金属M日交易额，写出y关于t的函数关系式，并求出这30天中第几日交易额最大，最大值为多少?

21．（本小题满分16分）

    已知圆O是以坐标原点为圆心，以1为半径的圆，直线l₁过点A（3，0），且与圆O相切．

（1）求直线l₁的解析式；

（2）设圆O与x轴交于P，Q两点，M是圆O上异于P，Q的任意一点，过点A且与x轴垂直的直线为l₂，直线PM交直线l₂于点P’，直线QM交直线l₂于点Q’．求证：以P’Q’为直径的圆C总过定点，并求出定点坐标．