
抚顺市2009届高考调研试题
数学试题 (理工类)
(本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.考试时间120分钟)
第Ⅰ卷(选择题,共6分)
一、选择题(本大题共12小题,每小题5分,共60分,四个选项中只有一项正确)
1.设复数 ,
, (
( ),若
),若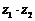 为实数,则
为实数,则 等于
等于
A. -2 B. -
2.已知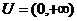 ,
,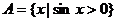 ,
, ,
,
A.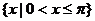 B.
B.
C.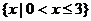 D.
D.
3.已知 、
、 是不共线的向量,
是不共线的向量,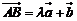 ,
, (
( 、
、 ),则
),则 、
、 、
、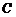 三点共线的充要条件是
三点共线的充要条件是
A. λ+μ=1 B.λ-μ=
4.设映射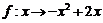 是实数集
是实数集 到实数集
到实数集 的映射,若对于实数
的映射,若对于实数 ,
,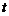 在
在 中不存在原象,则
中不存在原象,则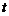 的取值范围是
的取值范围是
A.[1,+∞) B.(1,+∞) C.(-∞,1) D.(-∞,1]
5.“同一首歌”心连心文艺团体下基层进行宣传演出,原准备的节目表中有6个节目,如果保持这些节目的相对顺序不变,在它们之间再插入3个舞蹈节目,如果这三个舞蹈节目在节目表中既不排头,也不排尾,则不同的插入方法有( )种
A.200 B
6.已知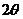 是第一象限的角,且
是第一象限的角,且 ,那么
,那么
A. B.
B. C.
C. D.
D.
7. 双曲线 (a>0,b>0)中,虚轴的两个端点与一个焦点恰好构成等边三角形,若虚轴长为2,则两条准线间的距离为
(a>0,b>0)中,虚轴的两个端点与一个焦点恰好构成等边三角形,若虚轴长为2,则两条准线间的距离为
A.  B.
B.  C.
C.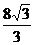 D.?
D.?
8.等差数列 中,
中, 是其前
是其前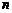 项和,
项和, ,
, ,则
,则 的值为
的值为
A.2006
B
9.设 、
、 、
、 为三个不同的平面,
为三个不同的平面,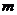 、
、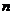 为两条不同的直线,在下列四个条件中:①
为两条不同的直线,在下列四个条件中:① ,
, ,
, ; ②
; ②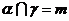 ,
, ,
, ;③
;③ ,
,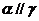 ,
, ; ④
; ④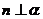 ,
,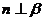 ,
, 。是
。是 的充分条件的有:
的充分条件的有:
A.①② B.②④ C.②③ D. ③④
10.已知点M(a,b)在由不等式组 所在平面区域的面积是
所在平面区域的面积是
A.8 B.
11.已知函数 (其中
(其中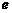 是自然对数的底数)的反函数为
是自然对数的底数)的反函数为 ,则有
,则有
A.  ?
? B.
B.  ?
?
C.  ?
? D.
D.  ?
?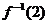
12.若不等式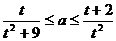 在
在 上恒成立,则
上恒成立,则 的取值范围是
的取值范围是
A. B.
B.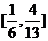 C.
C.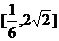 D.
D.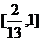
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 半径为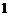 的球面上有
的球面上有 、
、 、
、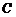 三点,其中点
三点,其中点 与
与 、
、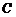 两点间的球面距离均为
两点间的球面距离均为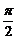 ,
, 、
、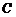 两点间的球面距离均为
两点间的球面距离均为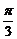 ,则球心到平面
,则球心到平面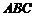 的距离为___ _ .
的距离为___ _ .
14.  展开式中,所有项的系数之和为 .
展开式中,所有项的系数之和为 .
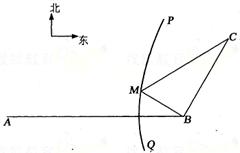 15.
15. 、
、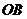 (
( 为原点)是圆
为原点)是圆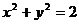 的两条互相垂直的半径,
的两条互相垂直的半径, 是该圆上任一点,且
是该圆上任一点,且 ,则
,则 .
.
16.如图,B地在A地的正东方向
地在B地的北偏东30°方向
的没岸PQ(曲线)上任意一点到A的距离
比到B的距离远
选一处M建一座码头,向B、C两地转运
货物.经测算,从M到B、M到C修建公
路的费用分别是a万元/km、
那么修建这两条公路的总费用最低是 .
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
已知向量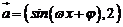 ,
, (
(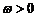 ,
,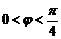 ).函数
).函数 ,
, 的图象的一个对称中心与它相邻的一条对称轴之间的距离为
的图象的一个对称中心与它相邻的一条对称轴之间的距离为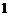 ,且过点
,且过点 .
.
(1)求函数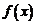 的表达式;
的表达式;
(2)当 时,求函数
时,求函数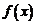 的单调区间。
的单调区间。
18.(本小题满分12分)
在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答这道题对的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是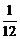 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是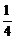 .
.
(1)求乙、丙两人各自回答这道题对的概率;
(2)用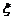 表示回答该题对的人数,求
表示回答该题对的人数,求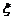 的分布列和数学期望
的分布列和数学期望 .
.
 19.(本小题满分12分)
19.(本小题满分12分)
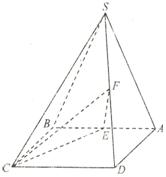
如图,四棱锥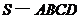 的底面
的底面 是正方形,侧面
是正方形,侧面
 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面,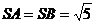 ,
,
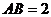 ,
,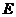 、
、 分别是
分别是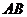 、
、 的中点。
的中点。
(1)求证: ;
;
(2)求二面角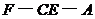 的大小。
的大小。
20.(本小题满分12分)
已知数列 中,
中,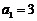 ,
, ,其前
,其前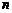 项和
项和 满足
满足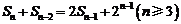 .令
.令 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若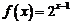 ,求证:
,求证: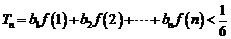 (
( );
);
21.(本小题满分12分)
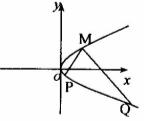 已知:点A(0,1),点R在y轴上运动, 点T在x轴上,N为动点,且
已知:点A(0,1),点R在y轴上运动, 点T在x轴上,N为动点,且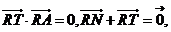
(1)设动点N的轨迹为曲线C,求曲线C的方程;
(2)如图所示:过点B(-2,0)的直线与曲线C交于点P、Q,
若在曲线C上存在点M,使得 是以PQ为斜边的直角三角形,求直线的斜率
是以PQ为斜边的直角三角形,求直线的斜率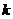 的取值范围。
的取值范围。
22.(本小题满分12分)
已知函数 .
.
(1)求函数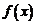 的单调区间和极值;
的单调区间和极值;
(2)若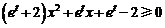 对满足
对满足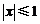 的任意实数
的任意实数 恒成立,求实数
恒成立,求实数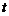 的取值范围(这里
的取值范围(这里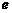 是自然对数的底数)
是自然对数的底数)
(3)求证:对任意正数 、
、 、
、 、
、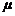 ,恒有:
,恒有:
 .
.
2009届调研试题数学一(理科)
一、选择题: C C D B D A A C B B A D

(2)由(Ⅰ) ,
, .
.
 的可能取值为:
的可能取值为: 、
、 、
、 、
、 .
.
则 ;
;
 ;
;
 ;
;
 .…………9分
.…………9分
∴ 的分布列为
的分布列为










 的数学期望
的数学期望 .…………12分
.…………12分
 故二面角
故二面角 的大小为
的大小为 …………………………12分
…………………………12分

解法二:如图,以 为原点,建立空间直角坐标系,使
为原点,建立空间直角坐标系,使 轴,
轴, 、
、 分别在
分别在 轴、
轴、 轴上。
轴上。

20.解:(1)由题意知 即
即 ……2分
……2分
∴
 ……5分
……5分
检验知 、
、 时,结论也成立,故
时,结论也成立,故 .…………6分
.…………6分
(2)由于 ,故
,故

 .…………12分
.…………12分
21.解:(1)设 ,由
,由 知:R是TN的中点,…………………1分
知:R是TN的中点,…………………1分
则T(-x,0),R(0,
 ),
), =O 则(-x,-
=O 则(-x,-  )?(1,-
)?(1,-  )=0………………3分
)=0………………3分
∴ 点N的轨迹曲线C的方程为: ……………5分
……………5分
(2)设直线 的方程为
的方程为 ,代入曲线C的方程
,代入曲线C的方程 得:
得:  此方程有两个不等实根,
此方程有两个不等实根,
 ……………6分
……………6分
M在曲线C上,P、Q是直线 与曲线C的交点,
与曲线C的交点,
设 则
则 ,
,
 是以PQ为斜边的直角三角形
是以PQ为斜边的直角三角形 ……8分
……8分
 ,
, ,有
,有
由于 ,
,
∴ ∴
∴ …………10分
…………10分
t为点M的纵坐标, 关于
关于 的方程
的方程 有实根,
有实根,

 ,
,
直线 的斜率
的斜率 且
且 ,
, 或
或 …12分
…12分
22.解(1)
∴ 的增区间为
的增区间为 ,
, 减区间为
减区间为 和
和 .…………3分
.…………3分
极大值为 ,极小值为
,极小值为 .…………5分
.…………5分
(2)原不等式可化为 由(1)知,
由(1)知, 时,
时, 的最大值为
的最大值为 .
.
∴ 的最大值为
的最大值为 ,由恒成立的意义知道
,由恒成立的意义知道 ,从而
,从而 …8分
…8分
(3)设
则 .
.
∴当 时,
时, ,故
,故 在
在 上是减函数,
上是减函数,
又当 、
、 、
、 、
、 是正实数时,
是正实数时,
∴ .
.
由 的单调性有:
的单调性有: ,
,
即 .…………12′
.…………12′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com