
甘肃省皋兰一中2009届高三5月份模拟考试(数学)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.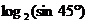 的值为( )
的值为( )
A.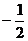 B.
B.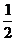 C.
C.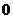 D.
D.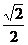
2.如果复数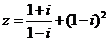 ,则
,则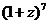 的展开式(按
的展开式(按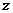 的升幂排列)的第5项是( )
的升幂排列)的第5项是( )
A .35 B.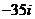 C.
C.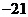 D.
D.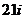
3.已知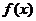 为偶函数,且
为偶函数,且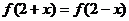 ,当
,当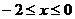 时,
时,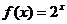 ,若
,若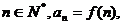 则
则
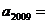 ( )
( )
A.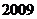 B.
B.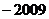 C.
C.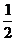 D.
D.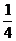
4.已知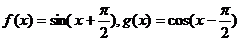 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.函数 的周期为
的周期为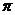 B.函数
B.函数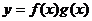 的最小值为
的最小值为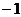
C.将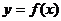 的图象向左平移
的图象向左平移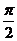 单位后得
单位后得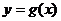 的图象
的图象
D.将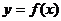 的图象向右平移
的图象向右平移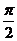 单位后得
单位后得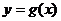 的图象
的图象
5.(理科)设斜率为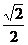 的直线
的直线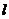 与椭圆
与椭圆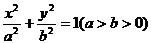 交于不同的两点。且这两点在
交于不同的两点。且这两点在 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )
轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )
A.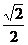 B.
B.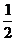 C.
C.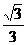 D.
D.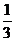
(文科)若抛物线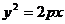 的焦点与双曲线
的焦点与双曲线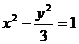 的右焦点重合,则
的右焦点重合,则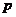 的值( )
的值( )
A.4 B.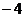 C.2 D.
C.2 D.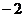
6.在样本的频率分布直方图中,共有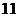 个小长方形,若其中一个小长方形的面积等于其他
个小长方形,若其中一个小长方形的面积等于其他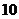 个小长方形面积和的四分之一,样本容量为
个小长方形面积和的四分之一,样本容量为 ,则该小长方形这一组的频数为( )
,则该小长方形这一组的频数为( )
A.32 B.
7.
已知函数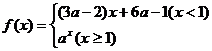 在
在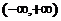 上单调递减,那么实数
上单调递减,那么实数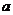 的取值范围是( )
的取值范围是( )
A. B.
B.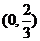 C.
C.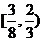 D.
D.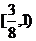
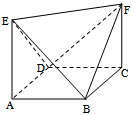 8.如右图所示的几何体ABCDEF中,ABCD是平行四边形且AE∥CF,
8.如右图所示的几何体ABCDEF中,ABCD是平行四边形且AE∥CF,
六个顶点任意两点连线能组成异面直线的对数是( )
A.36 B.28 C.39 D.20
9. 设实数 满足
满足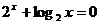 ,则有( )
,则有( )
A.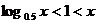 B.
B.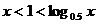 C.
C.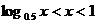 D.
D.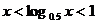
10.(理科)在平面直角坐标系中,已知点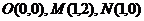 ,如果动点P满足
,如果动点P满足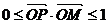 ,
,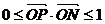 那么
那么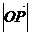 的最大值是( )
的最大值是( )
A.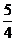 B.1 C.
B.1 C.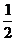 D.
D.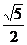
(文科)已知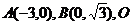 为坐标原点,点
为坐标原点,点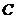 在
在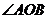 内,且
内,且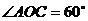 ,设
,设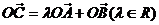 ,则
,则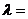 ( )
( )
A.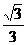 B.
B.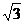 C.
C.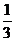 D.
D.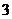
11.若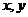 条件满足
条件满足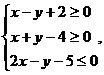 则
则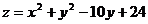 的最小值为( )
的最小值为( )
A.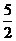 B.
B.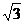 C.
C.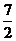 D.
D.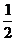
12. 已知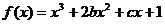 在区间
在区间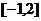 上是减函数,那么
上是减函数,那么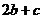 ( )
( )
A.有最大值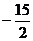 B.有最大值
B.有最大值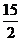 C.有最小值
C.有最小值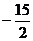 D.有最小值
D.有最小值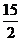
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.不等式(x-1)|x2-2x-3|≥0的解集为_________.
14.霓红灯的一个部位由七个小灯泡组成,如图:○○○○○○○,每个灯泡均可亮出红色或黄色,现设计每次变换只闪亮其中三个灯泡,且相邻两个不同时亮,则一共可呈现____________种不同的变换形式.(用数字作答)
15.(理科)已知 的三个顶点在同一球面上,
的三个顶点在同一球面上,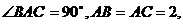 若球心
若球心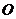 到平面
到平面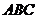 的距离为1,则该球的半径
的距离为1,则该球的半径
 (文科)设函数
(文科)设函数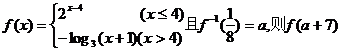 =
.
=
.
16.已知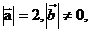 且关于
且关于 的函数
的函数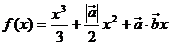 在
在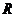 上有极值,则
上有极值,则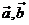 的夹角范围为
的夹角范围为
答题卡
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
题号
13
14
15
16
答案
三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
已知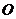 为坐标原点,
为坐标原点,
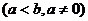 。
。
⑴求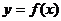 的单调递增区间;
的单调递增区间;
⑵若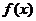 的定义域为
的定义域为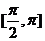 ,值域为
,值域为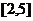 ,求
,求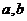 的值。
的值。
18.(本小题满分12分)
从北京到西安的某三列火车正点到达的概率分别为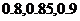 。求:
。求:
⑴这三列火车恰有两列正点到达的概率;
⑵(文科)这三列火车至少有两列误点到达的概率。
(理科)这三列火车正点到达列数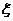 的数学期望。
的数学期望。
19.(本小题满分12分)
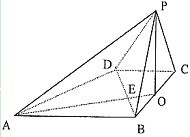
如图,已知四棱锥P―ABCD的底面是直角梯形,,AB=BC=PB=PC=2CD=2,侧面底面ABCD,O是BC中点,AO交BD于E。
(1)求证:;(2)求二面角的大小;
(3)求证:平面平面PAB。
20.(本题满分12分)
设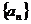 是正数组成的数列,其前
是正数组成的数列,其前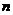 项和为
项和为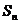 ,并且对于所有的正整数
,并且对于所有的正整数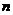 ,
,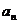 与
与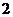 的等差中项等于
的等差中项等于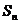 与
与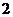 的等比中项。
的等比中项。
(1) 求数列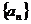 的通向公式;
的通向公式;
(2)(文科)令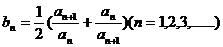 ,求数列
,求数列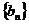 的前
的前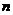 项和。
项和。
(理科)令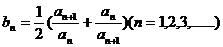 ,求
,求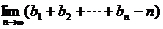 。
。
21. (本小题满分12分)
22. (本小题满分12分)
(理科)已知函数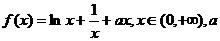 为实常数。
为实常数。
⑴若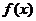 在
在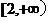 上是单调函数,求
上是单调函数,求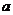 的取值范围;
的取值范围;
⑵当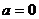 时,求
时,求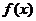 的最小值;
的最小值;
⑶设各项均为正数的无穷数列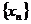 满足
满足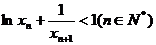 ,证明:
,证明: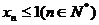 。
。
(文科)已知函数
⑴若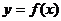 图像上的点
图像上的点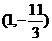 处切线的斜率为
处切线的斜率为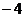 ,,求
,,求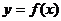 的极大值;
的极大值;
⑵若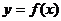 在区间
在区间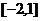 上是单调减函数,求
上是单调减函数,求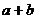 的最小值。
的最小值。
A;A;C;D;A;A; C;C;B;C(文)D(理);C;A
13、 或
或 ; 14、80; 15、(理)
; 14、80; 15、(理) (文)-2; 16、
(文)-2; 16、 ;
;
17、解:⑴
 ………………………………………3分
………………………………………3分
 时,由
时,由 得函数的递增区间为
得函数的递增区间为
 时,由
时,由 得函数的递增区间为
得函数的递增区间为
…………………………………………………………………………………………………………………5分
⑵
 …………………………………………………………7分
…………………………………………………………7分
 时,
时, 得:
得: (舍)
(舍)
 时,
时, 得
得
综上, ………………………………………………………………………………10分
………………………………………………………………………………10分
18、解:用 分别表示三列火车正点到达的事件,则
分别表示三列火车正点到达的事件,则

⑴恰有两列火车正点到达的概率记为 ,则
,则
 ……………………………………………6分
……………………………………………6分
⑵(文科)用 表示误点的列数,则至少两列误点可表示为:
表示误点的列数,则至少两列误点可表示为:

 ……………………………………………………………………………………12分
……………………………………………………………………………………12分
(理科)三列火车正点的列数分别为 。则
。则



 ……………………………………………………………10分
……………………………………………………………10分
 …………………………12分
…………………………12分
19.解:方法一:(I)证明:,
又 平面平面ABCD,平面平面ABCD=BC,
平面平面ABCD,平面平面ABCD=BC,

平面ABCD ……2分
在梯形ABCD中,可得
,即
在平面ABCD内的射影为AO, ……4分
(II)解:,且平面平面ABCD
平面PBC, 平面PBC,
为二面角P―DC―B的平面角 ……6分
是等边三角形即二面角P―DC―B的大小为 …8分
(III)证明:取PB的中点N,连结CN, ①
①
,且平面平面ABCD,平面PBC ……10分
平面PAB 平面平面PAB ②
由①、②知平面PAB…………..10分
连结DM、MN,则由MN//AB//CD, ,
,
得四边形MNCD为平行四边形,,平面PAB.
平面PAD 平面平面PAB ……………….12分
方法二:取BC的中点O,因为是等边三角形,
由侧面底面ABCD 得底面ABCD ……1分
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O―xyz……2分

(I)证明:,则在直角梯形中,
在等边三角形PBC中,……3分


 ,即…4分
,即…4分
(II)解:取PC中点N,则

平面PDC,显然,且平面ABCD
所夹角等于所求二面角的平面角 ……6分

 ,二面角的大小为 ……8分
,二面角的大小为 ……8分
(III)证明:取PA的中点M,连结DM,则M的坐标为
又 ……10分
……10分
 ,
,
 即
即
平面PAB,平面平面PAB ……12分
20.解:Ⅰ由已知得: …………………………………………………………2分
…………………………………………………………2分
当 解得:
解得: ……………………………………………………3分
……………………………………………………3分
当 时,
时, ,带入上式得:
,带入上式得:
配方得:
所以 ……………………………………………………………5分
……………………………………………………………5分
所以 ………………………………………………7分
………………………………………………7分
Ⅱ(文科)
 ……………………………………………………………………………………10分
……………………………………………………………………………………10分
 …………………………………12分
…………………………………12分
(理科)
 ………………………………………………………………………………9分
………………………………………………………………………………9分
 ……………………11分
……………………11分
 …………………………………………………………12分
…………………………………………………………12分
22.解:⑴ ;
;
当 时,
时, ;
;
令 ,该二次函数的对称轴为
,该二次函数的对称轴为
当 时,设
时,设 ,
, ,则
,则 ;
;
当 时,要使
时,要使 在
在 上是单调函数,只能为
上是单调函数,只能为 上的减函数
上的减函数
故函数 在
在 上满足:
上满足:
 或
或 ,解得
,解得 。综上
。综上 ………4分
………4分
⑵当 时,
时, ;
;
当 ;当
;当

所以 …………………………………………………4分
…………………………………………………4分
⑶反证法:不妨设 ,由⑵知
,由⑵知
所以
所以


所以 ;
;
因为 时,
时, 这与上面的结论矛盾,故
这与上面的结论矛盾,故
同理 ……………………………………………12分
……………………………………………12分
(文)解:⑴
则 ,所以
,所以 ……………………………3分
……………………………3分
 ;由此可知
;由此可知
当 时,函数
时,函数 单调递增
单调递增
当 时,函数
时,函数 单调递减,
单调递减,
当 时,函数取极大值
时,函数取极大值 ………………………………………………………………6分
………………………………………………………………6分
⑵ 在区间
在区间 上是单调减函数,
上是单调减函数,
所以 在区间
在区间 上恒成立,由二次函数的图像可知:
上恒成立,由二次函数的图像可知:
 ;令
;令 …………………………………………………9分
…………………………………………………9分
当直线 经过交点
经过交点 时,取得最小值
时,取得最小值 …………………………………12分
…………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com