
2009年汕头市濠江区高中阶段学校招生与初中毕业生学业模拟考试
数学科试卷
说明:1.本卷共4页,共24小题,考试时间100分钟,满分150分;
2.考生必须在答题卷中作答.
一、选择题(本大题共8小题,每小题4分,共32分,在每小题给出的四个选项中,只有一个是正确的,请将所选选项的字母填写在答卷中对应题号的空格内)
1、|-2|的相反数是( )
A.-2 B.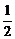 D.-
D.-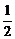
2.保护水资源,人人有责任,我国是缺水的国家,目前可利用的淡水资源的总量仅仅为899000亿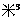 ,用科学计数法表示这个数是( )
,用科学计数法表示这个数是( )
A.0.899×106亿米3 B.8.99×105亿米3
C.8.99×104亿米3 D.8.99×103亿米3
3.由4个相同的小立方块搭成的几何体如图所示,它的左视图是( )
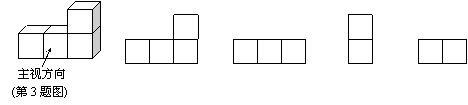 |
A B C D
4.体育老师对九年级(1)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成频数分布直方图(如图).由图可知,最喜欢篮球的频率是 ( )
A.0.16 B.
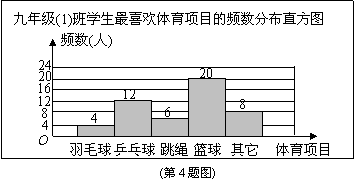 |
 5.如图,数轴上所表示的不等式组的解集是( )
5.如图,数轴上所表示的不等式组的解集是( )
A.x≤2 B.-1≤x≤2
C.-1<x≤2 D.x>-1
 6.下列图形中,既是中心对称图形又是轴对称图形的是
( )
6.下列图形中,既是中心对称图形又是轴对称图形的是
( )
A B C D
7.函数y=x和y=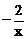 在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( )
 |
8.下列命题,正确的命题有几个?( )
(1)有一个角等于50o的两个等腰三角形一定相似;
(2)有一个角等于120o的两个等腰三角形一定相似;
(3)有一个锐角都等于20o的两个直角三角形相似;
(4)任意两个等边三角形一定相似
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共5小题,每小题4分,共20分)
9.-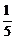 的倒数是
.
的倒数是
.
10.数据2、3、x、4的平均数是3,则这组数据的众数是 .
11.抛物线y=(x-1)2+3的对称轴是直线 .
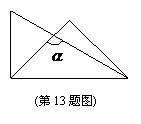 12.已知2
12.已知2 =2,2
=2,2 =4,2
=4,2 =8,2
=8,2 =16,2
=16,2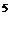 =32,2
=32,2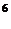 =64,……
=64,……
观察上面规律,试猜想2 的末位数是 .
的末位数是 .
13.一副三角板,如图13叠放在一起,则∠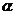 的度数是 度.
的度数是 度.
三、解答题(本大题共5小题,每小题7分,共35分)
14.求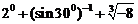 的值。
的值。
15.先化简 ,然后自选一个合适的x值,代入化简得到的式子求值。
,然后自选一个合适的x值,代入化简得到的式子求值。
16.为倡导绿色环保,某中学九年级(1)班计划组织部分同学义务植树180棵,由于同学们参与的积极性很高,实际参加植树活动的人数比原计划增加了50%,结果每人比原计划少栽了2棵树,问实际有多少人参加了这次植树活动?
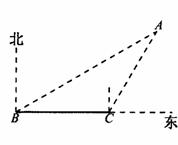
17.如图,已知灯塔A的周围7海里的范围内有暗礁,一艘渔轮在B处测得灯塔A在北偏
 东60°的方向,向正东航行8海里到C处后,又测得该灯塔在北偏东30°方向,渔轮不改变航向,继续向东航行,有没有触礁危险?请通过计算说明理由。(参考数据
东60°的方向,向正东航行8海里到C处后,又测得该灯塔在北偏东30°方向,渔轮不改变航向,继续向东航行,有没有触礁危险?请通过计算说明理由。(参考数据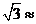 1.732)
1.732)
(第17题图)
 18、已知∠AOB和OB上点M,求作:⊙P,使它与
18、已知∠AOB和OB上点M,求作:⊙P,使它与
OA、OB都相切,且与OB的切点为M。
(要求尺规作图,保留作图痕迹,不要求写出作法)
(第18题图)
四、解答题(本大题共3小题,每小题9分,共27分)
19.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)小明认为口袋中共有三种颜色的球,所以从袋中任意摸出一球,摸到红球、白球
或黄球的概率都是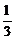 ,你认为对吗?请你用列表或画树状图的方法说明理由.
,你认为对吗?请你用列表或画树状图的方法说明理由.
20.已知二元一次方程: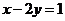 ,
,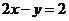 ,
,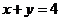 .请从这三个方程中选择你喜欢的两个方程,组成一个方程组,并求出这个方程组的解.
.请从这三个方程中选择你喜欢的两个方程,组成一个方程组,并求出这个方程组的解.
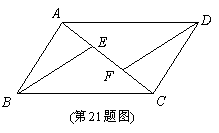
 21.如图,
21.如图,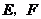 是平行四边形
是平行四边形 的对角线
的对角线 上的点,
上的点,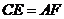 . 请你猜想:
. 请你猜想: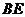 与
与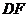 有怎样的位置关系和数量关系?
有怎样的位置关系和数量关系?
并对你的猜想加以证明.
猜想:
证明:
五、解答题(本大题共3小题,每小题12分,共36分)
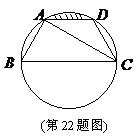
22. (本小题满分12分)
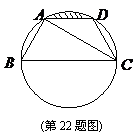 如图,已知点
如图,已知点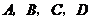 均在已知圆上,
均在已知圆上,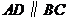 ,
, 平分
平分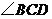 ,
, ,四边形
,四边形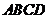 的周长为
的周长为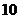 cm.
cm.
(1)求此圆的半径;
(2)求图中阴影部分的面积(其中л≈3,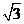 ≈1.7) 。
≈1.7) 。
 23. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
23. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
(1)由图观察易知A(0,2)关于直线l的对称点 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)
的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)
关于直线 l 的对称点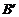 、
、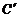 的位置,并写出他
的位置,并写出他
们的坐标: 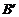 、
、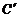 ;
;
(2)结合图形观察以上三组点的坐标,你会发现:坐
标平面内任一点P(a,b)关于第一、三象限的角平分
线 l 的对称点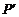 的坐标为 (不必证明);
(第23题图)
的坐标为 (不必证明);
(第23题图)
(3)已知两点D(1,-3)、E(-1,-4),试在直线 l 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
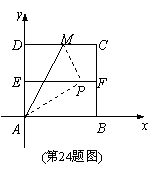
 24.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
24.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
(1)求点M、P的坐标;
(2)求折痕AM所在直线的解析式.
(3)设点H为直线AM上的点,是否存在这样的点H,
使得以H、A、P为顶点的三角形为等腰三角形,
若存在,请直接写出点H的坐标;若不存在,请说明理由.
(第24题图)
二、填空题(本大题共5小题,每小题4分,共20分)
9、 . 10、 .
11、 。 12、 . 13、 .
三、解答题(本大题共5个小题;共35分.解答应写出文字说明、证明过程或演算步骤)
14.
15.
16.
 17.
17.
 |
18.
四、解答题(本大题共3小题,每小题9分,共27分)
19.
20.
21.
 五、解答题(本大题共3小题,每小题12分,共36分)
五、解答题(本大题共3小题,每小题12分,共36分)
22.
24.
一、选择题
1.A 2.B 3.C 4.D 5.C 6.A 7.D 8.C
二、填空题
9.-5 10.3 11.x=1 12.2 13.105
三、解答题
14.解: 
= 1 + 2 + (-2) …………6分.
=1 …………7分.
15.解:由题意,得x-3>0,∴x>3, …………2分
∴原式= …………4分
…………4分
= …………5分.
…………5分.
=
= …………6分.
…………6分.
当x=4时,原式= …………7分
…………7分
提示:本题属开放题,答案不唯一。在选取x值时,注意必须符合x>3这一条件。
16.解:设原计划参加植树的学生有 人,则实际参加植树的学生有1.5
人,则实际参加植树的学生有1.5 ,依题意得:
,依题意得:
………2分
 …………5分
…………5分
解得 ,
,
经检验x=30是原方程的根,∴ …………6分
…………6分
答:实际参加这次植树的学生有45人. …………7分
17.解:作AD⊥BC交BC延长线于D, …………2分
 设AD=
设AD= ,在Rt△ACD中,∠CAD=30°
,在Rt△ACD中,∠CAD=30°
∴CD= 。 …………4分
。 …………4分
在Rt△ABD中,∠ABD=30°
∴BD= ∵BC=8
∵BC=8
x=4 ≈6.928 ∵6.928海里<7海里 …………6分
≈6.928 ∵6.928海里<7海里 …………6分
∴有触礁危险。
答:有触礁危险。 …………7分
18.根据具体情况给分。
四、解答题
19.解:(1)设红球的个数为 ,………………………………1分
,………………………………1分
由题意得, ……………………………4分
……………………………4分
解得,  .
.
答:口袋中红球的个数是1. ……………………………5分
 (2)小明的认为不对. ……………………………………6分
(2)小明的认为不对. ……………………………………6分
树状图如下:
…………8分
∴  ,
, ,
, .
.
∴ 小明的认为不对. …………9分
20.解:可组成方程组: ………………2分
………………2分
(1)+(2)得: ………………4分
………………4分
∴ ………………6分
………………6分
把 代入(2)得:
代入(2)得: ………………8分
………………8分
∴原方程组的解为 ………………9分
………………9分
答案不唯一,其它按此参考给分
21.猜想:BE∥DF BE=DF ………………4分.
证明:在平行四边形ABCD中,AB=CD、AB∥CD
∴∠BAC=∠DCA
又∵ AF=CE
∴AE=CF
∴△ABE≌△CDF ………………7分.
∴BE=DF ∠AEB=∠CFD
∴∠BEF=∠DFE
∴BE∥DF ………………9分.
五、解答题
 22..解:(1)
22..解:(1) ,
, °,
°,
 °. ……………2分
°. ……………2分
又 平分
平分 ,
,
 °.……………4分
°.……………4分
 ,
, °.
°.
 °, ………………6分
°, ………………6分
 是圆的直径,
是圆的直径, . ………………7分
. ………………7分
 四边形
四边形 的周长为
的周长为 cm,
cm,
 cm,
cm, cm.
cm.
 此圆的半径为
此圆的半径为 cm. ………………8分
cm. ………………8分
(2)设 的中点为
的中点为 ,由(1)可知
,由(1)可知 即为圆心.
即为圆心.
连接 ,过
,过 作
作 于
于 .……………9分
.……………9分
在 中,
中, ,
,
 cm.
cm.
 (cm2). ………………10分
(cm2). ………………10分
 ≈0.3(cm2)……12分
≈0.3(cm2)……12分
23. 解:(1) 如图: ,
, ;…………………………4分
;…………………………4分
(2) (b,a) ; …………………………6分
(3) 由(2)得,D(1,-3) 关于直线 l 的对称点 的坐标为(-3,1),连接
的坐标为(-3,1),连接 E交
E交
直线 l 于点Q,此时点Q到D、E两点的距离之和最小 ……………8分
 设过
设过 (-3,1) 、E(-1,-4)的直线的解析式为
(-3,1) 、E(-1,-4)的直线的解析式为 ,则
,则
 ,∴
,∴ ,
,
∴ .
…………………………10分
.
…………………………10分
由
 得
得
∴所求Q点的坐标为( ,
, ) …………12分
) …………12分
24.解:(1)依据题意
∵AP=AD=4,AE=2
∴EP=
∴P点坐标为(2 ,2) ……………………4分
,2) ……………………4分
设DM=x,则MP=x,过M作MN⊥EF,垂足为N,则MN=2,
PN=2 -x
-x
在Rt△MNP中,22+(2 -x)2=x2
-x)2=x2
解之得:x=
∴M点坐标为( ,4) ………8分
,4) ………8分
(2)设折痕AM所在直线的解析式为y=kx(k≠0),则4= k
k
k= ∴折痕AM所在直线的解析式为y=
∴折痕AM所在直线的解析式为y= x ………10分
x ………10分
(3)H1(-2,-2 ),H2(
),H2( ,2),H3(2,2
,2),H3(2,2 ),H4(2
),H4(2 ,6) ………12分
,6) ………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com