
安徽省马鞍山二中2009年四模考试
数学(文科)试题
一.选择题本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。.
2.已知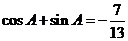 ,A为第二象限角,则tanA= .
,A为第二象限角,则tanA= .
A.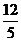 B.
B.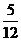 C.
C.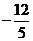 D.
D.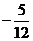
3.在数列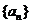 中,
中,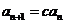
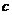 为非零常数.,且前
为非零常数.,且前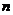 项和为
项和为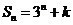 ,则实数
,则实数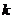 的值为 .
的值为 .
A.0
B.
4.在等腰直角三角形ABC中,若M是斜边AB上的点,则AM小于AC的概率为 .
A.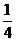 B.
B.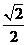 C.
C.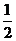 D.
D.
5.若关于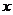 的不等式
的不等式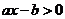 的解集是
的解集是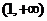 ,则关于
,则关于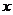 的不等式
的不等式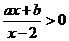 的解集是 .
的解集是 .
 A.
A.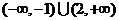 B.
B.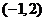
C.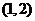 D.
D.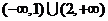
6.右面程序运行后,输出的值是 .
A.42 B.43 C.44 D.45
7.自点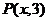 向圆
向圆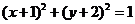 引切线,则切线长度的最小值等于 ..
引切线,则切线长度的最小值等于 ..
A.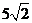 B.
B.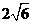 C.
C.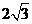 D.
D.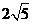
8.把正方形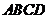 沿对角线
沿对角线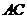 折起,当以
折起,当以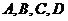 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线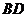 和平面
和平面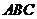 所成的角的大小为
所成的角的大小为
A.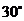 B.
B.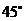 C.
C.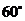 D.
D.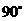
9.若关于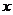 的方程
的方程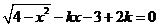 有且只有两个不同的实数根,则实数
有且只有两个不同的实数根,则实数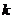 的
的
取值范围是
A.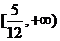 B.
B.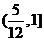 C.
C.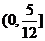 D.
D.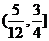
10.过椭圆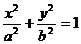
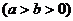 的左顶点
的左顶点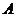 作斜率为1的直线,与椭圆的另一个交点为
作斜率为1的直线,与椭圆的另一个交点为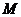 ,与
,与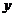 轴的交点为
轴的交点为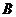 。若
。若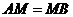 ,则该椭圆的离心率为 .
,则该椭圆的离心率为 .
A.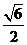 B.
B.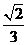 C.
C.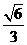 D.
D.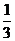
11.设函数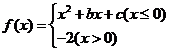 ,若f -4.=
f 0.,f -2 .= 0,则不等式
,若f -4.=
f 0.,f -2 .= 0,则不等式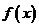 ≤ 1的解集为 .
≤ 1的解集为 .
A.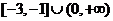 B.
B.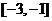
C.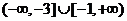 D.
D.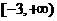
12.若方程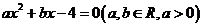 有两个实数根,其中一个根在区间1,2.内,则
有两个实数根,其中一个根在区间1,2.内,则 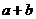 的取值范围是
的取值范围是
A.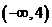 B.
B.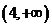 C.
C.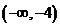 D.
D.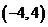
二.填空题:本大题共4小题,每小题4分,共16分.
 13.某大型超市销售的乳类商品有四种:纯奶.酸奶.婴幼儿奶粉.成人奶粉,且纯奶.酸奶.婴幼儿奶粉.成人奶粉分别有
13.某大型超市销售的乳类商品有四种:纯奶.酸奶.婴幼儿奶粉.成人奶粉,且纯奶.酸奶.婴幼儿奶粉.成人奶粉分别有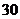 种.
种.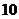 种.
种.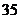 种.
种.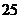 种不同的品牌.现采用分层抽样的方法从中抽取一个容量为
种不同的品牌.现采用分层抽样的方法从中抽取一个容量为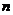 的样本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是
的样本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是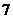 ,则
,则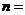 .
.
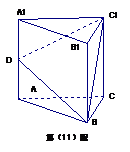
14.如图,在正三棱柱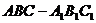 中,D为棱
中,D为棱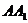 的中点,若截面
的中点,若截面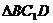 是面积为6的直角三角形,则此三棱柱的体积为
。
是面积为6的直角三角形,则此三棱柱的体积为
。
15.以下五个命题中,正确命题的序号是______________
①△ABC中,A>B的充要条件是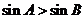 ;
;
②函数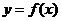 在区间1,2.上存在零点的充要条件是
在区间1,2.上存在零点的充要条件是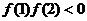 ;
;
 ③等比数列{a
③等比数列{a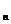 }中,
}中,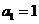 ,公比q>0, 则前n项和为
,公比q>0, 则前n项和为 ;
;
④把函数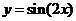 的图象向左平移
的图象向左平移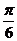 个单位后,得到的图象对应的解析式为
个单位后,得到的图象对应的解析式为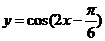 ;
;
⑤若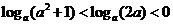 ,则a的取值范围为
,则a的取值范围为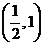 。
。
16.已知两点等分单位圆时,有相应正确关系为: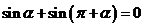 ;三点等分单位圆时,有相应正确关系为
;三点等分单位圆时,有相应正确关系为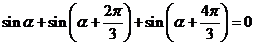 .由此可以推知四点等分单位圆时的相应正确关系:
。
.由此可以推知四点等分单位圆时的相应正确关系:
。
三.解答题:本大题共6小题,共74分,解答应写出文字说明.证明过程或演算步骤
17.本小题满分12分.已知向量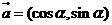 ,
,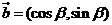 ,
,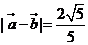 ,
,
1.求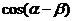 的值;
的值;
2.若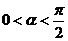 ,
,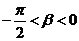 ,且
,且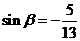 ,求
,求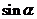 的值.
的值.
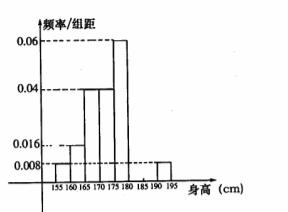
18.本小题满分12分.从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组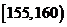 .第二组
.第二组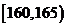 ;…第八组
;…第八组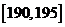 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组.第七组.第八组人数依次构成等差数列。
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组.第七组.第八组人数依次构成等差数列。
1.估计这所学校高三年级全体男生身高180cm以上含180cm.的人数;
2.求第六组.第七组的频率并补充完整频率分布直方图;
3.若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为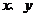 ,求满足:
,求满足: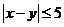 的事件概率。
的事件概率。
19.本小题满分12分.已知数列
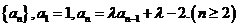
1.当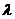 为何值时,数列
为何值时,数列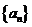 可以构成公差不为零的等差数列,并求其通项公式
可以构成公差不为零的等差数列,并求其通项公式
2.若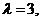 令
令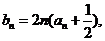 求数列
求数列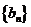 的前n项和
的前n项和
 20.本小题满分12分.如图,在四棱锥
20.本小题满分12分.如图,在四棱锥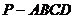 中,底面
中,底面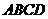 为菱形,
为菱形,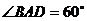 ,
, 为
为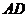 的中点。
的中点。
 1.若
1.若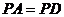 ,求证:平面
,求证:平面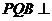 平面
平面 ;
;
2.点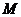 在线段
在线段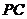 上,
上,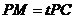 ,试确定实数
,试确定实数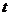 的值,使得PA∥平面
的值,使得PA∥平面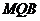 。
。
21.本小题满分12分.已知圆A :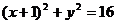 ,N为圆上的一动点,点B1,0.,点M是BN的中点,点P在线段AN上,且
,N为圆上的一动点,点B1,0.,点M是BN的中点,点P在线段AN上,且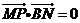 。
。
1.求动点P的轨迹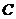 的方程;
的方程;
2.过A作一条与两坐标都不垂直的直线l交轨迹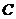 于P.Q两点,在x轴上是否存在点N,使得NF恰好为PNQ的内角评分线,若存在,求出点N的坐标,若不存在,请说明理由。
于P.Q两点,在x轴上是否存在点N,使得NF恰好为PNQ的内角评分线,若存在,求出点N的坐标,若不存在,请说明理由。
22.本小题满分14分.设函数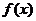
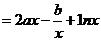 参考数据
参考数据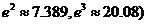
Ⅰ.若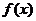 在
在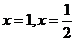 处取得极值,
处取得极值,
i .求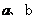 的值;
的值;
ii.在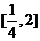 上存在
上存在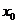 ,使得不等式
,使得不等式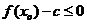 成立,求c的最小值
成立,求c的最小值
Ⅱ.当b=a时,若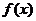 在
在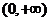 上是单调函数,求
上是单调函数,求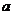 的取值范围。
的取值范围。
17.本题满分14分.已知函数 。
。
(1)
求函数 在
在 上的值域;
上的值域;
(2)
在 中,若
中,若 ,求
,求 的值。
的值。
16 
21.本小题满分12分.
已知函数fx.=lnx- ,
,
(I) 求函数fx.的单调增区间;
(II)
若函数fx.在[1,e]上的最小值为 ,求实数a的值。
,求实数a的值。



 3.已知
3.已知 ,则
,则 的值为 .
的值为 .
A.-2 B.-1 C.1 D.2
19.解:1.∵ ,
, ,
,
∴ ,
,
∵ ,
,
∴ ,
,
即 ,
, .
.
2.∵ ,
, ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,
∴

 ,
,
 .
.
20.此题主要考查数列.等差.等比数列的概念.数列的递推公式.数列前n项和的求法
同时考查学生的分析问题与解决问题的能力,逻辑推理能力及运算能力.
解:I.

Ⅱ.

 16.本题满分14分.
16.本题满分14分.
解:1.连 ,四边形
,四边形 菱形
菱形  ,
,







 为
为 的中点,
的中点, 
又

 ,
,

 2.当
2.当 时,使得
时,使得 ,连
,连 交
交 于
于 ,交
,交 于
于 ,则
,则 为
为 的中点,又
的中点,又
 为
为 边
边 上中线,
上中线,
 为正三角形
为正三角形 的中心,令菱形
的中心,令菱形 的边长为
的边长为 ,则
,则 ,
, 。
。




 即:
即:
 。
。
22.本小题满分14分.
解:I.1. ,
,
 。…………………………………………1分
。…………………………………………1分
 处取得极值,
处取得极值,
 …………………………………………………2分
…………………………………………………2分
即
 ………………………………………4分
………………………………………4分
ii.在
 ,
,
由

 ,
,

 ;
;
当
 ;
;

 ;
;
 .……………………………………6分
.……………………………………6分
面
 ,
,
且
又
 ,
,

 ……………9分
……………9分
Ⅱ.当 ,
,
① ;
;
②当 时,
时,
 ,
,

③ ,
,
从面得 ;
;
综上得, .………………………14分
.………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com