|
试题详情
10.已知函数f (x)= ,若方程f (x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是 ,若方程f (x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是 试题详情
试题详情
二、填空题:本大题共5小题,每小题5分,共25分。 11.已知复数z1=3-i,z2=2i-1, 是z的共轭复数,则复数 是z的共轭复数,则复数 的虚部等于_____。 的虚部等于_____。 试题详情
12.一个半径为1的球内切于正三棱柱,则该正三棱柱的体积为__________。 试题详情
13.已知x、y满足条件 ( k为常数),若z=x+3y的最大值为8,则k=__________。 ( k为常数),若z=x+3y的最大值为8,则k=__________。 试题详情
14.在三角形ABC中, ,M为BC边的中点,则中线AM的长为__________,△ABC的面积的最大值为__________。 ,M为BC边的中点,则中线AM的长为__________,△ABC的面积的最大值为__________。 试题详情
15.在数列{an}中,都有 ( p为常数),则称{an}为“等方差数列”。下列是对“等方差数列”的判断: ( p为常数),则称{an}为“等方差数列”。下列是对“等方差数列”的判断: 试题详情
⑴数列{an}是等方差数列,则数列 是等差数列; 是等差数列; 试题详情
⑵数列 是等方差数列; 是等方差数列; ⑶若数列{an}既是等方差数列,又是等差数列,则该数列必为常数列; ⑷若数列{an}是等方差数列,则数列{akn}( k为常数,k∈N*)也是等方差数列,则正确命题序号为______。 试题详情
三、解答题:
试题详情
试题详情
 17.下面玩掷骰子放球游戏,若掷出1点或6点,甲盒放一球;若掷出2点,3点,4点或5点,乙盒放一球,设掷n次后,甲、乙盒内的球数分别为x、y. 17.下面玩掷骰子放球游戏,若掷出1点或6点,甲盒放一球;若掷出2点,3点,4点或5点,乙盒放一球,设掷n次后,甲、乙盒内的球数分别为x、y.
⑴当n=3时,设x=3,y=0的概率; 试题详情
⑵当n=4时,设 ,求ξ的分布列及数学期望Eξ. ,求ξ的分布列及数学期望Eξ. 试题详情
18.(本小题满分12分)四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足 . . ⑴求证:PA⊥平面ABCD; ⑵求二面角E-AC-D的大小; ⑶在线段BC上是否存在点F使得PF∥面EAC?若存在,确定F的位置;若不存在,请说明理由。 试题详情
19.某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获取最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q (件)与实际销售价x (元)满足关系: 试题详情
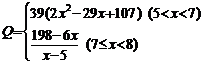
⑴求总利润(利润=销售额-成本) y (元)与实际销售价x (件)的函数关系式; ⑵试问:当实际销售价为多少元时,总利润最大. 试题详情
20.已知A(-1,0)、B(3,0),M、N是圆O:x2+y2=1上的两个动点,且M、N关于x轴对称,直线AM与BN交于P点. ⑴求P点的轨迹C的方程; 试题详情
试题详情
21.已知数列{an}满足: , , . . 试题详情
⑴求数列{an}的通项公式; ⑵证明: ; ; 试题详情
⑶设 ,且 ,且 ,证明: ,证明: . . 湖北省八市2009年高三年级三月调考 试题详情
一、选择题 1.B 2.A 3.C 4.B 5.B 6.D 7.C 8.C 9.D 10.A 二、填空题 11. 12. 12. 13.-6 14. 13.-6 14. ; ; 15.①②③④ 15.①②③④ 三、解答题 16.解:⑴ = = = = = = = 3分 3分  = = =1+1+2cos2x=2+2cos2x=4cos2x =1+1+2cos2x=2+2cos2x=4cos2x
∵x∈[0, ] ∴cosx≥0 ] ∴cosx≥0 ∴ =2cosx 6分 =2cosx 6分 ⑵ f (x)=cos2x- ?2cosx?sinx=cos2x- ?2cosx?sinx=cos2x- sin2x sin2x =2cos(2x+ ) 8分 ) 8分 ∵0≤x≤ ∴ ∴ ∴ ∴ ∴ ∴ ∴ ,当x= ,当x= 时取得该最小值 时取得该最小值  ,当x=0时取得该最大值 12分 ,当x=0时取得该最大值 12分 17.由题意知,在甲盒中放一球概率为 时,在乙盒放一球的概率为 时,在乙盒放一球的概率为 2分 2分 ①当n=3时,x=3,y=0的概率为 4分 4分 ②当n=4时,x+y=4,又|x-y|=ξ,所以ξ的可能取值为0,2,4 (i)当ξ=0时,有x=2,y=2,它的概率为 4分 4分 (ii)当ξ=2时,有x=3,y=1或x=1,y=3 它的概率为 (iii)当ξ=4时,有x=4,y=0或x=0,y=4 它的概率为 故ξ的分布列为 ξ 0 2 4 10分 p 


∴ξ的数学期望Eξ= 12分 12分  18.解:⑴证明:在正方形ABCD中,AB⊥BC 18.解:⑴证明:在正方形ABCD中,AB⊥BC
又∵PB⊥BC ∴BC⊥面PAB ∴BC⊥PA 同理CD⊥PA ∴PA⊥面ABCD 4分 ⑵在AD上取一点O使AO= AD,连接E,O, AD,连接E,O, 则EO∥PA,∴EO⊥面ABCD 过点O做 OH⊥AC交AC于H点,连接EH,则EH⊥AC, 从而∠EHO为二面角E-AC-D的平面角 6分 在△PAD中,EO= AP= AP= 在△AHO中∠HAO=45°, 在△AHO中∠HAO=45°, ∴HO=AOsin45°= ,∴tan∠EHO= ,∴tan∠EHO= , , ∴二面角E-AC-D等于arctan 8分 8分 ⑶当F为BC中点时,PF∥面EAC,理由如下: ∵AD∥2FC,∴ ,又由已知有 ,又由已知有 ,∴PF∥ES ,∴PF∥ES ∵PF 面EAC,EC 面EAC,EC 面EAC ∴PF∥面EAC, 面EAC ∴PF∥面EAC, 即当F为BC中点时,PF∥面EAC 12分 19.⑴据题意,得 4分 4分  5分 5分
⑵由⑴得:当5<x<7时,y=39(2x3-39x2+252x-535) 
当5<x<6时,y'>0,y=f (x)为增函数 当6<x<7时,y'<0,y=f (x)为减函数 ∴当x=6时,f (x)极大值=f (16)=195 8分 当7≤x<8时,y=6(33-x)∈(150,156] 当x≥8时,y=-10(x-9)2+160 当x=9时,y极大=160 10分 综上知:当x=6时,总利润最大,最大值为195 12分 20.⑴设M(x0,y0),则N(x0,-y0),P(x,y)
(x0≠-1且x0≠3) BN:y= ② ② 联立①② ∴ 4分 4分 ∵点M(xo,yo)在圆⊙O上,代入圆的方程: 整理:y2=-2(x+1) (x<-1) 6分 ⑵由 设S(x1、y1),T(x2、y2),ST的中点坐标(x0、y0) 则x1+x2=-(3+ ) ) x1x2= 8分 8分 ∴ 中点到直线 的距离 的距离 
∴ 故圆与x=- 总相切. 13分 总相切. 13分 ⑵另解:∵y2=-2(x+1)知焦点坐标为(- ,0) 2分 ,0) 2分 顶点(-1,0),故准线x=- 4分 4分 设S、T到准线的距离为d1,d2,ST的中点O',O'到x=- 的距离为 的距离为 又由抛物线定义:d1+d2=|ST|,∴ 故以ST为直径的圆与x=- 总相切 8分 总相切 8分 21.解:⑴由 ,得 ,得 令 ,有 ,有 ∴ = = 又b1=2a1=2, 3分 3分 ∴ ∴ 4分 4分 ⑵证法1:(数学归纳法) 1°,当n=1时,a1=1,满足不等式 5分 5分 2°,假设n=k(k≥1,k∈N*)时结论成立 即 ,那么 ,那么 即 7分 7分 又 由1°,2°可知,n∈N*,都有 成立 9分 成立 9分 ⑵证法2:由⑴知: (可参照给分) (可参照给分) ∵ , , ,∴ ,∴ ∵ ∵ ∵ ∴ ∴ ∴ 当n=1时, ,综上 ,综上 ⑵证法3: 
∴{an}为递减数列 当n=1时,an取最大值 ∴an≤1 由⑴中知  综上可知 ⑶ 欲证: 即证 即证 11分 11分 即ln(1+Tn)-Tn<0,构造函数f (x)=ln(1+x)-x ∵ 当x>0时,f ' (x)<0 当x>0时,f ' (x)<0 ∴函数y=f (x)在(0,+∞)内递减 ∴f (x)在[0,+∞)内的最大值为f (0)=0 ∴当x≥0时,ln(1+x)-x≤0 又∵Tn>0,∴ln(1+Tn)-Tn<0 ∴不等式 成立 14分 成立 14分
| | | 

 的值是
的值是 B.
B. C.1 D.-
C.1 D.-
 B.±
B.± C.±
C.± D.32
D.32 =1的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若A、B和双曲线的一个顶点构成的三角形为锐角三角形,则该双曲线的离心率e的取值范围是
=1的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若A、B和双曲线的一个顶点构成的三角形为锐角三角形,则该双曲线的离心率e的取值范围是 ) B.(1,
) B.(1, ) C.(
) C.( -1,1+
-1,1+ ) D.(1,2)
) D.(1,2)