
等于
。
试题详情
14.四棱锥P―ABCD的顶点P在底面ABCD中的投影恰好是A, 其三视图如右图,则四棱锥P―ABCD的表面积为
。 试题详情
15.若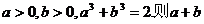 的最大值为
。 的最大值为
。 试题详情
16.曲线C由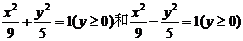 两部分组成,若过点(0,2)作直线l与曲线C有且仅有两个公共点,则直线l的斜率的取值范围为
。 两部分组成,若过点(0,2)作直线l与曲线C有且仅有两个公共点,则直线l的斜率的取值范围为
。 试题详情
17.定义在(-1,1)上的函数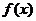 满足: 满足: 试题详情
(i)对任意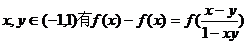 , , 试题详情
(ii)当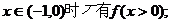 试题详情
若 试题详情
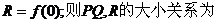 (用“<”连接) (用“<”连接) 试题详情
三、解答题:本大题有5小题,共72分,解答应写出文字说明,证明过程或演算步骤。
试题详情
已知向量 试题详情
(I)求函数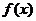 的最小正周期和图象的对称轴方程; 的最小正周期和图象的对称轴方程; 试题详情
(II)求函数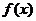 在区间 在区间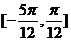 上的值域。 上的值域。 试题详情
试题详情
某校篮球选修课的考核方式采用远距离投离篮进行,规定若学生连中于球,则通过考核,终止投篮;否则继续投篮,直至投满四次终止。现有某位同学每次投篮的命中率为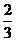 ,且每次投篮相互经独立。 ,且每次投篮相互经独立。 (I)该同学投中二球但未能通过考核的概率; 试题详情
(II)现知该校选修篮球的同学共有27位,每位同学每次投篮的命中率为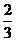 ,且每次投篮相互独立。在这次考核中,记通过的考核的人数为X,求X的期望。 ,且每次投篮相互独立。在这次考核中,记通过的考核的人数为X,求X的期望。 试题详情
20. (本题满分14分)
如图所示的几何体是以正三角形ABC为底面的直棱柱(侧棱垂直于底面的棱柱)被平面DEF所截而得,AB=2,BD=1,CE=3,AF=a,T为AB的中点。 (I)当a=5时,求证:TC//平面DEF; (II)当a=4时,求平面DEF与平面ABC相交所成且为锐角的二面角的余弦值; (III)当a为何值时,在DE上存在点P,使CP⊥平面DEF? 试题详情
试题详情
试题详情
已知椭圆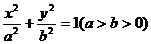 的离心率为 的离心率为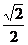 ,椭圆上任意一点到右焦点F的 ,椭圆上任意一点到右焦点F的 试题详情
距离的最大值为 (1)求椭圆的方程; (2)已知点C(m,0)是线段OF上的一个动点(O为坐标原点),是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得|AC|=|BC|,并说明理由。 试题详情
试题详情
已知函数 试题详情
(I)求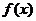 在[0,1]上的极值; 在[0,1]上的极值; 试题详情
(II)若对任意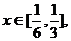 不等式 不等式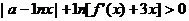 恒成立,求实数a的取值范围。 恒成立,求实数a的取值范围。 试题详情
(III)若函数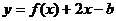 在[0,1]上恰有两个不同的零点,求实数b的取值范围。 在[0,1]上恰有两个不同的零点,求实数b的取值范围。 试题详情
一、选择题: 1―5 ACBBD 6―10 BCDAC 二、填空题: 11.60 12. 13.― 13.― 14.
14. 15.2 16. 17. 17. 三、解答题: 18.解:(I)
20090506 (II)由于区间 的长度是为 的长度是为 ,为半个周期。 ,为半个周期。
又 分别取到函数的最小值 分别取到函数的最小值 所以函数 上的值域为 上的值域为 。……14分 。……14分 19.解:(1)该同学投中于球但未通过考核,即投蓝四次,投中二次,且这两次不连续,其概率为 …………5分
…………5分 (2)在这次考核中,每位同学通过考核的概率为
 ………………10分 ………………10分
随机变量X服从 其数学期望 其数学期望  …………14分 …………14分
20.解:(1)设FD的中点为G,则TG//BD,而BD//CE,

当a=5时,AF=5,BD=1,得TG=3。
又CE=3, TG=CE。 TG=CE。  四边形TGEC是平行四边形。 四边形TGEC是平行四边形。  CT//EG, CT//EG, TC//平面DEF,………………4分 TC//平面DEF,………………4分
(2)以T为原点,以射线TB,TC,TG分别为x,y,z轴, 建立空间直角坐标系,则D(1,0,1),  ………………6分
………………6分

则平面DEF的法向量n=(x,y,z)满足:
解之可得 又平面ABC的法向量 又平面ABC的法向量 m=(0,0,1)
 即平面DEF与平面ABC相交所成且为锐角的二面角的余弦值为 ……9分 ……9分 (3) 由P在DE上,可设 由P在DE上,可设 ,……10分 ,……10分
则
 ………………11分 ………………11分
若CP⊥平面DEF,则 即
解之得: ……………………13分
……………………13分
即当a=2时,在DE上存在点P,满足DP=3PE,使CP⊥平面DEF。…………14分 21.解:(1)因为 所以 所以
椭圆方程为: ………………4分
………………4分 (2)由(1)得F(1,0),所以 。假设存在满足题意的直线l,设l的方程为 。假设存在满足题意的直线l,设l的方程为

代入 ………………6分 ………………6分
设 ① ①
 ……………………8分 ……………………8分
设AB的中点为M,则
 。 。
 ……………………11分 ……………………11分
 ,即存在这样的直线l; ,即存在这样的直线l;
当 时, k不存在,即不存在这样的直线l;……………………14分 时, k不存在,即不存在这样的直线l;……………………14分 22.解:(I) ……………………2分 ……………………2分
令 (舍去) (舍去)
 单调递增; 单调递增;
当 单调递减。 ……………………4分 单调递减。 ……………………4分
 为函数 为函数 在[0,1]上的极大值。 ……………………5分 在[0,1]上的极大值。 ……………………5分 (II)由 得 得  ① ………………………7分 ① ………………………7分
设 , , 依题意知 上恒成立。 上恒成立。 

 都在 都在 上单调递增,要使不等式①成立, 上单调递增,要使不等式①成立,
当且仅当 …………………………11分 …………………………11分
(III)由 令 ,则 ,则 当 上递增; 上递增; 当 上递减; 上递减; 而 

 …………………………16分 …………………………16分
| | | | | | | | | 


 棱台的体积公式:
棱台的体积公式:
 h表示棱台的高
h表示棱台的高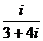 在复平面上对应的点位于 ( )
在复平面上对应的点位于 ( ) 则,该命题的否定是 ( )
则,该命题的否定是 ( )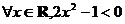 B.
B.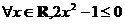
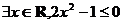 D.
D.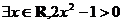
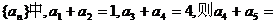 ( )
( )