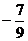山东省聊城市2009年高三年级高考模拟(二)
数学试题(理科)
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分。考试时间120分钟。
2.答第Ⅰ卷前,考生务必用黑色签字笔将自己的姓名、准考证号、考试科目涂写在答题卡和试题纸上。
3.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试题卷上。
4.第II卷写在答题纸对应区域内,严禁在试题卷或草纸上答题。
5.考试结束后,将答题卡和答题纸一并交回。
参考公式:
1.若事件A、B互斥,则
2.若事件A、B相互独立,则
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,,每小题5分,共60分。在每小题给出的四个选项中,选出一个符合题目要求的选项)
1.已知全集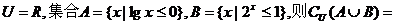 ( )
( )
试题详情
试题详情
2.已知抛物线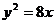 的焦点与双曲线
的焦点与双曲线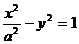 的一个焦点重合,则该双曲线的离心率为 ( )
的一个焦点重合,则该双曲线的离心率为 ( )
试题详情
试题详情
3.已知关于x的二项式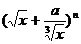 展开式的二项式系数之和为32,常数项为80,则a的值为 ( )
展开式的二项式系数之和为32,常数项为80,则a的值为 ( )
试题详情
A.1 B.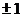 C.2 D.
C.2 D.
试题详情
4.若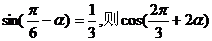 的值为 ( )
的值为 ( )
试题详情
试题详情
|
试题详情
A.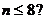 B. B.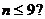 试题详情
C.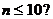 D. D. 试题详情
6.若直线 试题详情
截得的弦最短,则直线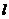 的方程是( ) 的方程是( ) 试题详情
A.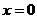 B. B. 试题详情
C.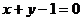 D. D. 试题详情
7.设函数 试题详情

A.0 B.1
试题详情
C.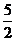 D.5 D.5 试题详情
8.已知函数 的图像 的图像 试题详情
|
试题详情
9.已知直线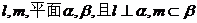 ,给出下列四个命题 ,给出下列四个命题 试题详情
①若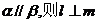 ;②若 ;②若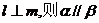 ;③若 ;③若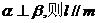 ;④若 ;④若 其中正确命题的个数是 ( ) A.0 B.1 C.2 D.3 试题详情
10.已知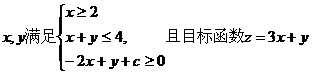 的最小值是5,则z的最大值是 的最小值是5,则z的最大值是 ( ) A.10 B.12 C.14 D.15 试题详情

A.6种 B.12种 C.18种 D.24种
试题详情
12.已知关于x的不等式 有唯一的整数解, 有唯一的整数解, 试题详情
则方程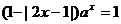 实数根的个数为 ( ) 实数根的个数为 ( ) A.0 B.1 C.2 D.3 第Ⅱ卷(非选择题
共90分)
|
试题详情
13.已知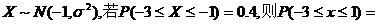 。 。 试题详情
14.在R上定义运算 对一切实数x都成立,则实数a的取值范围是 。 对一切实数x都成立,则实数a的取值范围是 。 试题详情
15.在区间[1,4]上任取实数a,在区间[0,3]上任取实数b,使函数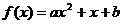 有两个相民间零点的概率是
。 有两个相民间零点的概率是
。 试题详情
16.下列说法正确的是 。(写出所有正确说法的序号) 试题详情
①若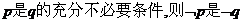 的必要不充分条件; 的必要不充分条件; 试题详情
②命题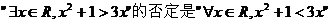 ; ; 试题详情
③设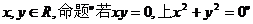 的否命题是真命题; 的否命题是真命题; 试题详情
④若 试题详情
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤) 17.在 分别是角A、B、C的对边, 分别是角A、B、C的对边,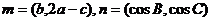 ,且 ,且 (1)求角B的大小; 试题详情
(2)设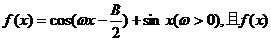 的最小正周期为 的最小正周期为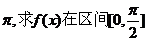 上的最大值和最小值。 上的最大值和最小值。 试题详情
18.甲、乙两人同时参加奥运志愿者的选拔赛,已知在备选的10道题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选。 试题详情
(1)求甲答对试题数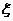 的分布列及数学期望; 的分布列及数学期望; (2)求甲、乙两人至少有一人入选的概率。 试题详情

(1)求证:AE//平面DCF;
试题详情
(2)当AB的长为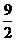 , ,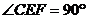 时,求二面角A―EF―C的大小。 时,求二面角A―EF―C的大小。 试题详情
20.设数列 试题详情
(1)求
|
试题详情
21.已知椭圆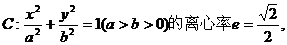 左、右焦点分别为F1、F2,点 左、右焦点分别为F1、F2,点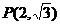 ,点F2在线段PF1的中垂线上。 ,点F2在线段PF1的中垂线上。 (1)求椭圆C的方程; 试题详情
(2)设直线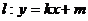 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为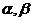 ,且 ,且 ,求证:直线 ,求证:直线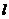 过定点,并求该定点的坐标。 过定点,并求该定点的坐标。 试题详情
22.已知函数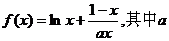 为大于零的常数。 为大于零的常数。 试题详情
(1)若函数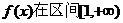 内调递增,求a的取值范围; 内调递增,求a的取值范围; 试题详情
(2)求函数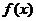 在区间[1,2]上的最小值。 在区间[1,2]上的最小值。 试题详情
(3)求证:对于任意的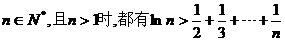 成立。 成立。 试题详情
一、选择题:本大题共12个小题,每小题5分,共60分。 1―6BBCDBD 7―12CACAAC 二、填空题:本大题共4个小题,每小题4分,共16分。 13.0.8; 14. 15. ; ; 16.①③ 三、解答题: 17.解:(1)由 , , 得  由正弦定得,得  又B  又 又 6分
6分 (2) 由已知  9分
9分 当 因此,当 时, 时,  当 , ,  12分 12分 18.解:(1)依题意,甲答对主式题数 的可能取值为0,1,2,3,则 的可能取值为0,1,2,3,则     4分 4分  的分布列为 的分布列为  0 1 2 3 P 



甲答对试题数 的数学期望为 的数学期望为  6分 6分 (2)设甲、乙两人考试合格的事件分别为A、B,则   9分 9分 因为事件A、B相互独立,  甲、乙两人考试均不合格的概率为 甲、乙两人考试均不合格的概率为   甲、乙两人至少有一人考试合格的概率为 甲、乙两人至少有一人考试合格的概率为  答:甲、乙两人于少有一人考试合格的概率为 12分 12分 另解:甲、乙两人至少有一个考试合格的概率为  答:甲、乙两人于少有一人考试合格的概率为 19.解法一(1)过点E作EG 交CF于G, 交CF于G,

// 所以AD=EG,从而四边形ADGE为平行四边形 故AE//DG 4分 因为 平面DCF, 平面DCF,  平面DCF, 平面DCF, 所以AE//平面DCF 6分 (2)过点B作 交FE的延长线于H, 交FE的延长线于H, 连结AH,BH。 由平面 , ,

所以 为二面角A―EF―C的平面角 为二面角A―EF―C的平面角 在  又因为 所以CF=4,从而BE=CG=3。 于是 10分 10分 在 则 , , 因为

解法二:(1)如图,以点C为坐标原点, 建立空间直角坐标系 设 则  于是 20.解:(1)当 时,由已知得 时,由已知得  同理,可解得 4分 4分 (2)解法一:由题设 当 代入上式,得 (*) 6分
(*) 6分 由(1)可得 由(*)式可得 由此猜想: 8分 8分 证明:①当 时,结论成立。 时,结论成立。 ②假设当 时结论成立, 时结论成立, 即 那么,由(*)得  所以当 时结论也成立, 时结论也成立, 根据①和②可知,  对所有正整数n都成立。 对所有正整数n都成立。 因 12分 12分 解法二:由题设 当 代入上式,得 6分 6分    -1的等差数列, -1的等差数列,   12分 12分 21.解:(1)由椭圆C的离心率 得 ,其中 ,其中 , , 椭圆C的左、右焦点分别为 又点F2在线段PF1的中垂线上  解得  4分 4分 (2)由题意,知直线MN存在斜率,设其方程为 由 消去 设 则 且 8分 8分 由已知 , , 得 化简,得 10分
10分  整理得  直线MN的方程为 直线MN的方程为 , , 因此直线MN过定点,该定点的坐标为(2,0) 12分 22.解: 2分 2分 (1)由已知,得 上恒成立, 上恒成立, 即 上恒成立 上恒成立 又 当 当  4分 4分 (2)当 时, 时,  在(1,2)上恒成立, 在(1,2)上恒成立, 这时 在[1,2]上为增函数 在[1,2]上为增函数  当  在(1,2)上恒成立, 在(1,2)上恒成立, 这时 在[1,2]上为减函数 在[1,2]上为减函数  当 时, 时, 令 又   9分 9分 综上, 在[1,2]上的最小值为 在[1,2]上的最小值为 ①当 ②当 时, 时, ③当 10分 10分 (3)由(1),知函数 上为增函数, 上为增函数, 当  即 恒成立 12分 恒成立 12分     恒成立 14分 恒成立 14分
| | | | | | | | | | | | | | | | | | | | | |



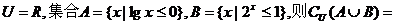 ( )
( )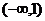 B.
B.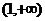 C.
C.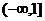 D.
D.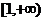
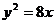 的焦点与双曲线
的焦点与双曲线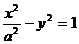 的一个焦点重合,则该双曲线的离心率为 ( )
的一个焦点重合,则该双曲线的离心率为 ( ) B.
B.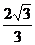 C.
C.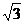 D.3
D.3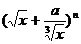 展开式的二项式系数之和为32,常数项为80,则a的值为 ( )
展开式的二项式系数之和为32,常数项为80,则a的值为 ( )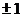 C.2 D.
C.2 D.
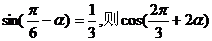 的值为 ( )
的值为 ( )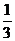 B.
B.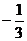 C.
C.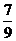 D.
D.