
假期复习第五天―――指、对数函数,二次函数
一.这几个概念你掌握了吗?请回顾一遍:
1.指数式与对数式的互化: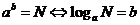
2.复习指数、对数的运算性质、换底公式。
3.掌握指数函数与对数函数的概念、图象和性质;并能利用指数函数与对数函数的单调性解题.
4.掌握二次函数的概念、图象及性质; 快速的作出图象。
5.二次函数的解析式的三种形式:一般式,顶点式,两根式.
6.二次函数、一元二次方程及一元二次不等式之间的灵活转化.
二.特别要注意下列方法:
1.重视指数式与对数式的互化;
2.不同底的对数运算问题,应化为同底对数式进行运算;
3.运用指、对数的公式解题时,要注意公式成立的前提.
4.同底的指数函数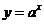 与对数函数
与对数函数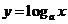 互为反函数
互为反函数
5.解决与对数函数有关的问题,要特别重视定义域;
6.指数函数、对数函数的单调性决定于底数大于1还是小于1,要注意对底数的讨论;
7.比较几个数的大小的常用方法有:
①以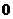 和
和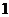 为桥梁;②利用函数的单调性;③作差.
为桥梁;②利用函数的单调性;③作差.
8.讨论二次函数的区间最值问题:①注意对称轴与区间的相对位置;②函数在此区间上的单调性;
9.讨论二次函数的区间根的分布情况一般需从三方面考虑:①判别式;②区间端点的函数值的符号;③对称轴与区间的相对位置.
三.下列习题你必须掌握:
1.已知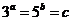 ,且
,且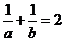 ,求
,求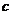 的值.
的值.
2.(1)若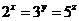 ,且
,且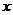 ,
, ,
,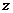 都是正数,则
都是正数,则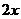 ,
,
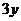 ,
,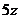 从小到大依次为
;
从小到大依次为
;
(2)设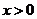 ,且
,且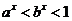 (
(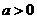 ,
,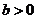 ),则
),则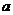 与
与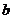 的大小关系是 ( )
的大小关系是 ( )
A.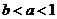 B.
B.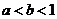 C.
C.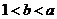 D.
D.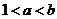
3.已知函数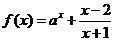
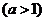 ,
,
用定义证明:函数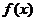 在
在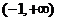 上为增函数;
上为增函数;
4.函数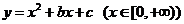 是单调函数的充要条件是
是单调函数的充要条件是
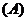
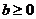
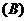
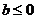
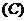
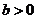
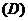
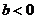
5.若函数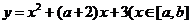 的图象关于
的图象关于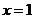 对称则
对称则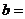 .
.
6.已知二次函数的对称轴为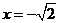 ,截
,截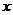 轴上的弦长为
轴上的弦长为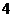 ,且过点
,且过点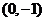 ,求函数的解析式。
,求函数的解析式。
7.已知函数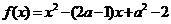 与非负
与非负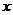 轴至少
轴至少
有一个交点,求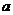 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com