
假期复习第十四天―――不等式
一.这几个概念你掌握了吗?请回顾一遍:
1. 不等式的基本性质有哪些?
2.均值不等式及其它几个重要不等式是否很熟练;
3.如何用分析法、综合法、比较法等证明简单的不等式;
4.分式不等式、二次不等式、对指数不等式、含绝对值不等式怎么解?
5.绝对值不等式的性质是什么,怎么样理解?
二.特别要注意下列方法:
1.比较法是不等式证明中最基本、也是最常用的方法,比较法的一般步骤是:作差(商)→变形→判断符号(值).
2.在解不等式中,换元法和图解法是常用的技巧之一.通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数、数形结合,则可将不等式的解化归为直观、形象的图形关系,对含有参数的不等式,运用图解法可以使得分类标准明晰;
3.不等式应用问题体现了一定的综合性.这类问题大致可以分为两类:一类是建立不等式、解不等式;另一类是建立函数式求最大值或最小值.利用平均值不等式求函数的最值时,要特别注意“正数、定值和相等”三个条件缺一不可,有时需要适当拼凑,使之符合这三个条件.利用不等式解应用题的基本步骤:10审题,20建立不等式模型,30解数学问题,40作答。
三.下列习题你必须掌握:
1、不等式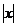 〉
〉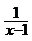 的解集是
的解集是
A.(-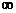 ,1)
B.(-
,1)
B.(-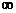 ,1)
,1)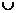 (1,
(1,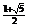 )
)
C.(- ,1)
,1)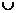 (
(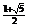 ,+
,+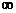 )
D.(-
)
D.(-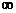 ,0)
,0)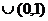
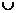 (
(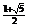 +
+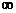 )
)
2、下列各组命题中,M是N的充要条件的是
A.M: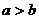 ;N:
;N: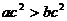 B.M:
B.M: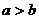 ,
,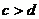 ;N:
;N: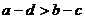
C.M: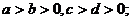 N:
N: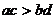 D.
D.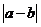 =
=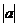 +
+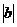 ;N:
;N: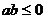
3、不等式组
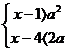 有解,则实数a的取值范围是
有解,则实数a的取值范围是
A.(-1,3)
B.(-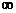 ,-1)
,-1)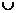 (3,+
(3,+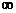 )
)
C.(-3,1)
D.(-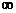 ,-3)
,-3)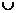 (1,+
(1,+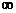 )
)
4、若 ,
,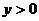 且
且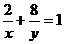 ,则
,则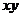 有
有
A.最大值64 B.最小值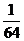 D.最小值
D.最小值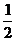
5、若不等式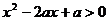 对
对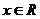 恒成立,则关于
恒成立,则关于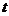 的不等式
的不等式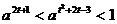 的解为
的解为
A.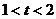 B.
B.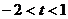 C.
C.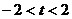 D.
D.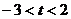
1. 不等式的基本性质有:
(1)对称性:a>b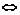 b<a;
b<a;
(2)传递性:若a>b,b>c,则a>c;
(3)可加性:a>b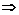 a+c>b+c,
a+c>b+c,
(4)可乘性:a>b,当c>0时,ac>bc;当c<0时,ac<bc。
2.不等式运算性质:
(1)同向相加:若a>b,c>d,则a+c>b+d;
(2)正数同向相乘:若a>b>0,c>d>0,则ac>bd。
(3)乘(开)方法则:若a>b>0,n∈N+,则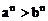 (
(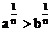 );
);
(4)倒数法则:若ab>0,a>b,则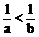 。
。
3.重要不等式
(1)a2+b2≥2ab(a,b∈R)
(2)当a,b≥0时,a+b≥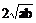
或ab≤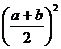
(3)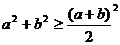
4.均值不等式的性质:
||a|-|b||≤|a+b|≤|a|+|b|
(1)ab≥0Û|a+b|=|a|+|b|
(2)ab<0Û|a+b|<|a|+|b|
(3)ab≤0Û|a+b|=||a|-|b||
(4)ab>0Û|a+b|>||a|-|b||
6、设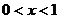 ,则函数
,则函数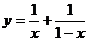 的最小值为 _____
的最小值为 _____
7、不等式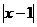 <
<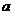 成立的充分条件是
成立的充分条件是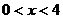 ,则
,则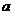 的取值范围是______
的取值范围是______
8、已知有向线段PQ的起点P和终点Q的坐标分别为(-1,1)和(2,2),直线L: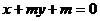 与PQ的延长线的相交,则
与PQ的延长线的相交,则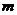 的取值范围是 ____
的取值范围是 ____
9.已知x≥0、y≥0,求证: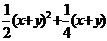 ≥
≥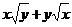
(请用多种方法做)
10.解关于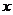 的不等式
的不等式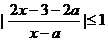
11.已知f(x)=-3x2+a(6-a)x+b
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a,b的值。
12.已知A、B两地相距200千米,一只船从A地逆水到
B地,水速为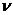 千米/
千米/
小时(8<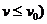 。若船每小时的燃料费与其在静水中的
。若船每小时的燃料费与其在静水中的
速度的平方成正比,当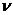 =
=
为720元,为了使全程燃油费最省,船的实际速度应为多
少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com