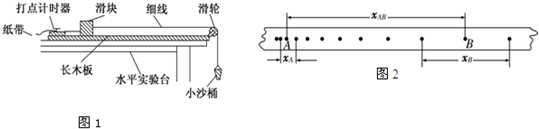
(1)如图1是验证动能定理的装置,除图示器材外,还有打点计时器所用的学生电源、导线、复写纸,天平和细沙.
①你认为还需要的实验器材有
刻度尺
刻度尺
.
②实验时为了保证滑块受到的合力与沙和沙桶的总重力大小基本相等,应满足的实验条件是
沙和沙桶的总质量远小于滑块的质量
沙和沙桶的总质量远小于滑块的质量
,实验时首先要做的步骤是
平衡摩擦力
平衡摩擦力
.
③图2是滑块(质量为M)在沙和沙桶的总质量为m条件下做匀加速直线运动的纸带.测量数据已用字母表示在图中,打点计时器的打点周期为T.则本实验最终要验证的数学表达式为
.(用题中的字母表示)
(2)某同学做“验证机械能守恒定律”实验
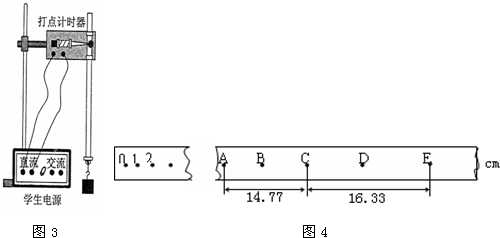
①该同学开始实验时情形如图3所示,接通电源释放纸带.请指出该同学在实验操作中存在的两处明显错误或不当的地方:
(i)
接错直流电源
接错直流电源
;(ii)
重物离打点计时器太远
重物离打点计时器太远
.
②该同学经修改错误后,在正确操作下,研究从静止开始下落的物体所受阻力的情况,得到如图4所示的纸带(A、B、C、D、E均为相邻的打点),测出A、C间的距离为14.77cm,点C、E间的距离为16.33cm.已知当地重力加速度为10m/s
2,电源的频率为50Hz,重锤质量为m=1.0kg,设重锤所受阻力大小不变.在从A下落到E的过程中,通过C点时的即时速度大小为
3.89
3.89
m/s,阻力大小为
0.25
0.25
N.(结果均保留三位有效数字)

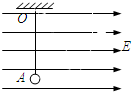
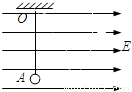
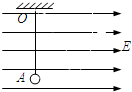 已知如图,匀强电场方向水平向右,场强E=1.5×106V/m,丝线长l=40cm,上端系于O点,下端系质量为m=1.0×10-4kg,带电量为q=+4.9×10-10C的小球,将小球从最低点A由静止释放,求:
已知如图,匀强电场方向水平向右,场强E=1.5×106V/m,丝线长l=40cm,上端系于O点,下端系质量为m=1.0×10-4kg,带电量为q=+4.9×10-10C的小球,将小球从最低点A由静止释放,求: