
题目列表(包括答案和解析)
.在“验证机械能守恒定律”的实验中,已知打点计时器所用电源的频率为50 Hz,查得当地重力加速度g=9.80 m/s2,测得所用的重物的质量为1.00 kg.实验中得到一条点迹清晰的纸带(如图实-4-9所示),把第一个点记作O,另选连续的四个点A、B、C、D作为测量的点.经测量知道A、B、C、D各点到O点的距离分别为62.99 cm,70.18 cm,77.76 cm,85.73 cm.根据以上数据,可知重物由O点运动到C点,重力势能的减少量等于________ J,动能的增加量等于________J(取三位有效数字).
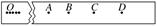
【解析】:根据测量数据,重物从O点运动到C点下落的高度h=0.7776 m,故重力势能减
少量
ΔEp=mgh=1.00×9.80×0.7776 J=7.62 J
重物动能的增加量ΔEk=mvC2-mv02
根据实验情况,重物在O点的速度v0=0,C点的速度vC等于重物从B点到D点这一
段时间Δt=2× s内的平均速度.由实验数据可得
vC== m/s=3.8875 m/s
重物的动能增加量
ΔEk=mvC2=×1.00×3.88752 J=7.56 J.
.在“验证机械能守恒定律”的实验中,已知打点计时器所用电源的频率为50 Hz,查得当地重力加速度g=9.80 m/s2,测得所用的重物的质量为1.00 kg.实验中得到一条点迹清晰的纸带(如图实-4-9所示),把第一个点记作O,另选连续的四个点A、B、C、D作为测量的点.经测量知道A、B、C、D各点到O点的距离分别为62.99 cm,70.18 cm,77.76 cm,85.73 cm.根据以上数据,可知重物由O点运动到C点,重力势能的减少量等于________ J,动能的增加量等于________J(取三位有效数字).
【解析】:根据测量数据,重物从O点运动到C点下落的高度h=0.7776 m,故重力势能减
少量
ΔEp=mgh=1.00×9.80×0.7776 J=7.62 J
重物动能的增加量ΔEk=mvC2-mv02
根据实验情况,重物在O点的速度v0=0,C点的速度vC等于重物从B点到D点这一
段时间Δt=2× s内的平均速度.由实验数据可得
vC== m/s=3.8875 m/s
重物的动能增加量
ΔEk=mvC2=×1.00×3.88752 J=7.56 J.

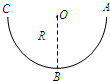 如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.
如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.| 1 |
| 2 |
| 2gR |
| v2 |
| R |
| gR |
| 1 |
| 2 |
| 2gR |
| v2 |
| R |
| gR |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com