答案：(1)如图

(2)答：这条船继续前进，没有被浅滩阻碍的危险。

解：作CD⊥直线AB于点D，

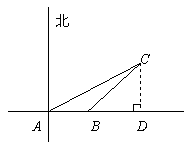         由已知可得∠CAD=30°, ∠CBD=45°，

         AB=100米。

         设CD=米。

         在Rt△ACD中

         tan∠CAD=

         ∴AD=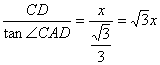

          在Rt△CBD中

         ∵∠CBD=45°, ∴BD=CD=x，

         ∵AD-BD=AB， ∴。

         解得

∴这条船继续前进没有被浅滩阻碍的危险。

答案：解：过D作DM⊥AE于M，过C作CN⊥AE于N，则：MN=CD=3米，设AM=x，则AN=x+3， 由题意：∠ADM =30^ｏ，∠ACN =45^ｏ，

在Rt△ADM中，DM=AM·cot30^ｏ=x，在Rt△ANC中，CN=AN=x+3，

又DM=CN=MB，∴x=x+3，解之得，x=（+1），∴AB=AM+MB=x+x+3=2×（+1）+3=3+6≈11（米）

解答题

某城市改造一块长为a米，宽为b米的矩形荒地，计划在矩形荒地上，修筑宽度为2米的两条互相垂直的道路，余下的四块矩形小场地建成草坪．

(1)如图，已知a∶b＝2∶1，并且四块草坪的面积之和为312平方米试求原来矩形荒地的长与宽．

(2)在(1)的条件下，某施工设计单位根据实际情况对整个矩形荒地作如下设计(要求同时符合下述两个条件)

条件①：在每块草坪上修建一个面积尽可能大的菱形花圃(花圃各边分别与所在草坪的对角线平行)并且其中有两个花圃的面积之差为13平方米．

条件②：整个矩形场地(包括道路，草坪，花圃)为轴对称图形．

请画出符合上述设计方案的一种草图，并求出每个菱形花圃的面积(不必说明画法与根据)．

在宽为6厘米的矩形纸带上，用菱形设计如下图所示的图案．如果菱形的边长为5厘米，请你回答下列问题：

（1）如果用6个这样的菱形设计图案，那么至少需要多长的纸带？
（2）设菱形的个数为x，所需的纸带长为y，试求y和x之间的函数关系式；
（3）现有长为250厘米的纸带，要设计这样的图案，最多设计多少个菱形？