（1）如图1，在等边△ABC中，∠1=∠2，求∠APN的度数；
（2）如图2，在正方形ABCD中，∠1=∠2，则∠APN=；
如图3，在正五边形ABCDE中，∠1=∠2，则∠APN=；
（3）如图4，在正n边形ABCDE…Q中，∠1=∠2，则∠APN=．（用含有n的式子表示）

（1）画图探究：
如图1，若点A、B在直线m同侧，在直线m上求作一点P，使AP+BP的值最小，保留作图痕迹，不写作法；
（2）实践运用：
如图2，在等边△ABC中，AB=2，点E是AB的中点，AD是高，点P是高AD上一个动点，求BP+PE的最小值
（3）拓展延伸：
如图3，四边形ABCD中，∠BAD=125°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小，并求此时∠MAN的度数．

15、已知，E、F分别是正多边形相邻两边上的点，且CE=BF，AF交BE于P，如图1，在等边△ABC中，有∠EPA=60°；如图2，在正方形ABCD中，有∠EPA=90°；如图3在正五边形ABCDM中，有∠EPA=108°；依此规律，在正八边形中，有∠EPA=度．

（2013•衢州）【提出问题】
（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．
【类比探究】
（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
【拓展延伸】
（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

（2013•宜兴市二模）阅读下面材料：
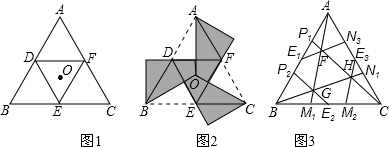
小明同学遇到这样一个问题：定义：如果一个图形绕着某定点旋转一定的角度α （0°＜α＜360°） 后所得的图形与原图形重合，则称此图形是旋转对称图形．如等边三角形就是一个旋转角为120°的旋转对称图形．如图1，点O是等边三角形△ABC的中心，D、E、F分别为AB、BC、CA的中点，请你将△ABC分割并拼补成一个与△ABC面积相等的新的旋转对称图形．小明利用旋转解决了这个问题（如图2所示）．图2中阴影部分所示的图形即是与△ABC面积相等的新的旋转对称图形．请你参考小明同学解决问题的方法，利用图形变换解决下列问题：
如图3，在等边△ABC中，E₁、E₂、E₃分别为AB、BC、CA 的中点，P ₁、P₂，M₁、M₂，N₁、N₂分别为AB、BC、CA的三等分点．
（1）在图3中画-个和△ABC面积相等的新的旋转对称图形，并用阴影表示（保留画图痕迹）；
（2）若△ABC的边长为6，则图3中△ABM₁的面积为．
（3）若△ABC的面积为a，则图3中△FGH的面积为．