
题目列表(包括答案和解析)
| x2 |
| 36 |
| y2 |
| 9 |
抛物线 =2x,经过焦点的抛物线的弦中点的轨迹方程为
=2x,经过焦点的抛物线的弦中点的轨迹方程为
[ ]
A. =x-1 B.
=x-1 B. =2(x-1)
=2(x-1)
C. =x-
=x-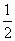 D.
D. =2x-1
=2x-1
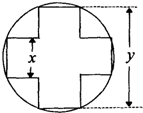 (2012•河北模拟)一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有4
(2012•河北模拟)一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有4| 5 |
 cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.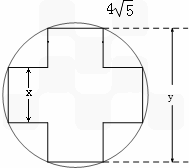
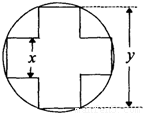 一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有
一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有 cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com