
题目列表(包括答案和解析)
 sA=
sA=| AD |
| b |
| 3 |
在人教版教材七年级下册第10章“实数”的数学活动1中,教科书介绍了“对于任意一个直角三角形,都有两条直角边的平方和等于斜边的平方”,这就是著名的“勾股定理”.勾股定理是自然界最本质最基本的规律之一,很多文明古国对此都有所研究,古希腊科学家毕达哥拉斯在公元前550年左右发现了这个定理,而我国早在公元前1 100多年就有人在使用这个定理来解决实际问题.
在自然数中有很多数都符合这个定理的形式,例如,32+42=52,52+122=132,92+402=412,72+242=252……
如果把自然数的范围扩大为有理数(整数和分数),你还能找出符合上面形式的有理数吗?如果再把有理数范围扩大为实数(有理数和无理数)范围呢?
 都可以写成两个单位分数的和:
都可以写成两个单位分数的和: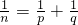 (n,p,q都是正整数).显然,这里的p,q都大于n.如果设p=n+a,q=n+b,那么有
(n,p,q都是正整数).显然,这里的p,q都大于n.如果设p=n+a,q=n+b,那么有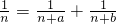 .
. ,
, 等于两个单位分数之和的所有可能情况;
等于两个单位分数之和的所有可能情况;
| 1 |
| n |
| 1 |
| n |
| 1 |
| p |
| 1 |
| q |
| 1 |
| n |
| 1 |
| n+a |
| 1 |
| n+b |
| 1 |
| 2 |
| 1 |
| 3 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com