
题目列表(包括答案和解析)
知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
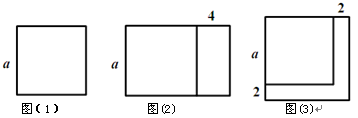
知识应用:图⑴是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为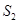
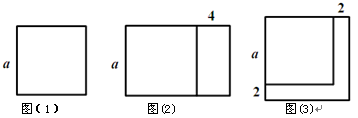
①用含a的代数式表示 ,
,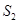 (需要化简)
(需要化简)
②请你用作差法比较 与
与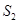 大小
大小
知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
知识应用:图⑴是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为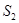

①用含a的代数式表示 ,
,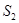 (需要化简)
(需要化简)
②请你用作差法比较 与
与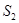 大小
大小
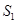 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
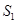 ,
, (需要化简)
(需要化简)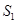 与
与 大小
大小知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
知识应用:图⑴是边长为a的正方形,将正方形一边![]() 不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为
不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为![]() ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为![]()
①用含a的代数式表示![]() ,
,![]() (需要化简)
(需要化简)
 ②请你用作差法比较
②请你用作差法比较![]() 与
与![]() 大小
大小
图(1) 图(2) 图(3)
将一个分数的分子、分母同时加上一个正数,这个分数变大了吗?先用一组具体的数来做一些试验:
![]() →
→![]()
![]() →
→![]()
![]() →
→![]()
![]() →
→![]()
-![]() →-
→-![]()
-![]() →-
→-![]()
(1)当这个分数是正的真分数时,分数变大;
(2)当这个分数是正的假分数时,分数变小;
(3)当这个分数是负分数时,结论刚好与上述相反.
以上结论是通过一些具体的数归纳出来的,但是我们不可能把所有数都拿出来一一验证这些结论是否正确.因此,在数学中把这种未经严格证明而只是从一些具体的数中归纳出来的规律,叫做“猜想”.猜想可能是对的,也可能是错的.要肯定上述结论是对的,必须用字母表示任意的数,利用代数式来证明它们.你能证明上述结论吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com