
题目列表(包括答案和解析)
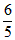 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
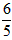 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
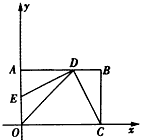
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;已知:如图,在平面直角坐标系![]() 中,矩形OABC的边OA在
中,矩形OABC的边OA在![]() 轴的正半轴上,OC在
轴的正半轴上,OC在![]() 轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。

(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与![]() 轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为![]() ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由。
已知,BC//OA,![]() B=
B=![]() A=100°,试回答下列问题:
A=100°,试回答下列问题:
(1)如下图所示,求证:OB//AC。
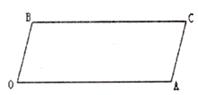
(2)如下图,若点E、F在BC上,且满足![]() FOC=
FOC= AOC,并且OE平分
AOC,并且OE平分![]() BOF。
BOF。
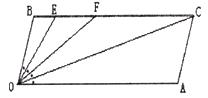
(i)求:![]() EOC的度数;
EOC的度数;
(ii)求:![]() OCB:
OCB:![]() OFB的值。
OFB的值。
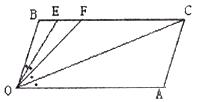
(iii)如下图,若![]() OEB=
OEB= OCA,此时
OCA,此时![]() OCA度数等于 。(在横线上填上答案即可)。
OCA度数等于 。(在横线上填上答案即可)。
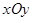 中,矩形OABC的边OA在
中,矩形OABC的边OA在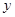 轴的正半轴上,OC在
轴的正半轴上,OC在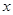 轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。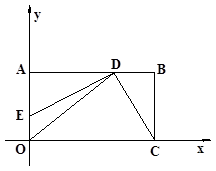
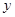 轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为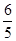 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com