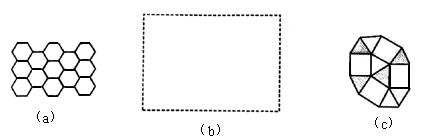
（1）如果只限于一种正多边形镶嵌，（如图（a）：正六边形镶嵌）

①在上述（a～g）七种图形中不能进行镶嵌的有________；（填字母序号）

②任选其中一个图形（正六边形除外）在（b）框中画出一个镶嵌图形；

（2）如果两种边数不同的正多边形镶嵌（如图（c）：正三角形与正方形镶嵌）以正三角形和正六边形镶嵌，则在一顶点周围有________个正三角形和________个正六边形；

（3）如果用边数为m、n、r、t、g（m、n、r、t、q互不相等）的五种正多边形各一个，恰好组成镶嵌图形，求的值。

挂不起来的红灯：

辅导员小G老师召开七年级各班文娱委员会议，要求各班在自己教室里布置游艺室，挂上十盏红灯，用五条笔直的彩带相连，并助理每条彩带连结四盏红灯，结果每个教室里的红灯彩带都布置成五角星形．小G老师说：“小R，请你帮五个班级出出主意，要求每个教室布置得各有特色，各不相同．”小R欣然同意，等到小G老师到各教室里一看，果然十分满意，说：“小R只把五角星中的一条边上下移动一下，就组成下列五个图形．”

接着，小G老师又说：“如果把十盏红灯编成1、2、3、4、5、6、7、8、9、10十个不同的号码．小R，你能使每条彩带上四盏红灯的数字和都相等吗？”

小R想了一想说：“这十盏灯挂不起来．”大家惊奇地说：“为什么？”小R说：“1＋2＋3＋4＋5＋6＋7＋8＋9＋10＝55．现在每个数字出现2次，所以五条彩带上的总和是110，110÷4不是整数，所以这不是难题，而是不可能的问题．”

小G老师接着说：“把十盏红灯拿走一盏，剩下九盏红灯，挂成十行，每行挂三盏，如果也把红灯标上1，2，3，4，5，6，7，8，9九个数字，试问每行上的三个字之和相等吗？

大家哈哈地笑了，小R说：“小G老师真会老题翻新，九个数字之和为45，每行三个数字之和应为15，而从9出发的行上只有9＋1＋5＝15，9＋4＋2＝15，再也找不到第三个符合条件的算式，其中有一个是9．”大家报以热烈的掌声．

聪明的同学们，闹了半天，你会不会把不标数字的九盏红灯挂成十行，每行三盏？试画出图来．

我国是最早了解和应用勾股定理的国家之一，古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用，古希腊数学家毕达哥拉斯首先证明了勾股定理，在西方，勾股定理又称为“毕达哥拉斯定理”．
关于勾股定理的研究还有一个很重要的内容是勾股数组，在《几何》课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：
方法1：若m为奇数（m≥3），则a=m，b=（m²-1）和c=（m²+1）是勾股数．
方法2：若任取两个正整数m和n（m＞n），则a=m²-n²，b=2mn，c=m²+n²是勾股数．
（1）在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
（2）请根据方法1和方法2按规律填写下列表格：

（3）某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树______棵．