
题目列表(包括答案和解析)
| 3 | 4 |
为了解某班学生喜爱打羽毛球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
|
|
|
50 |
已知在全部50人中随机抽取1人抽到不喜爱打羽毛球的学生的概率
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打羽毛球与性别有关?说明你的理由;
(3)已知喜爱打羽毛球的10位女生中, 还喜欢打篮球,
还喜欢打篮球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生 和
和 不全被选中的概率.下面的临界值表供参考:
不全被选中的概率.下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 .)
.)
【解析】第一问利用数据写出列联表
第二问利用公式 计算的得到结论。
计算的得到结论。
第三问中,从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
 ,
,
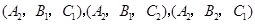 ,
,
基本事件的总数为8
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得
解:(1) 列联表补充如下:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
(2)∵
∴有99.5%的把握认为喜爱打篮球与性别有关
(3)从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
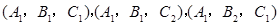 ,
,
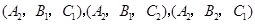 ,
,
基本事件的总数为8,
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得 .
.
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
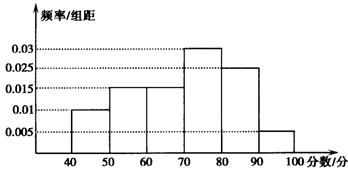
⑴80~90这一组的频数、频率分别是多少?
⑵估计这次环保知识竞赛的及格率(60分及以上为及格). (本小题满分10分)
【解析】本试题主要考查了统计和概率的综合运用。
第一问频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
第二问0.015×10+0.025×10+0.03×10+0.005×10=0.75
解:(1)频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
(2)0.015×10+0.025×10+0.03×10+0.005×10=0.75
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当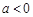 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
(1)已知不等式ax2+bx+c>0的解集为{x|α<x<β,α∈R+},求不等式cx2+bx+a<0的解集.
(2)已知集合A={x|2x2+7x-15<0},B={x|x2+ax+b≤0},满足A∩B=![]() ,A∪B={x|-5<x≤2},求实数a,b的值.
,A∪B={x|-5<x≤2},求实数a,b的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com