
题目列表(包括答案和解析)
6.已知地球半径约为6.4×106m,已知月球绕地球的运动近似看作匀速圆周运动,则可估算出月球到地心的距离约为_____m.(结果只保留一位有效数字)
5.如图1-4-6所示,直线Bb与曲线AB相切于B.一带电粒子(不计重力)在方向与纸面平行的匀强电场中沿曲线AB运动,当它到达B点时,电场突然改变方向而不改变大小.此后粒子的运动情况是[ ]
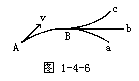
A.可能沿曲线Ba运动 B.可能沿直线Bb运动
C.可能沿曲线Bc运动 D.可能沿原曲线返回到A点
4.可以发射一颗这样的人造地球卫星,使其圆轨道 [ ]
A.与地球表面上某一纬度线(非赤道)是共面同心圆
B.与地球表面上某一经度线所决定的圆是共面同心圆
C.与地球表面上的赤道线是共面同心圆,且卫星相对地球表面是静止的
D.与地球表面上的赤道线是共面同心圆,但卫星相对地球表面是运动的
3.两颗人造卫星A、B绕地球做匀速圆周运动,周期之比为TA∶TB=1∶8,则轨道半径之比和运动速率之比分别为 [ ]
A.RA∶RB=4∶1,vA∶vB=1∶2
B.RA∶RB=4∶1,vA∶vB=2∶1
C.RA∶RB=1∶4,vA∶vB=1∶2
D.RA∶RB=1∶4,vA∶vB=2∶1
2.从倾角为θ的足够长的斜面上的A点,先后将同一小球以不同的初速度水平向右抛出.第一次初速度为v1,球落到斜面上的瞬时速度方向与斜面夹角为α1,第二次初速度为v2,球落到斜面上的瞬时速度方向与斜面夹角为α2,若v1>v2,则 [ ]
A.α1>α2 B.α1=α2
C.α1<α2 D.无法确定
1.做平抛运动的物体,每秒的速度增量总是 [ ]
A.大小相等,方向相同 B.大小不等,方向不同
C.大小相等,方向不同 D.大小不等,方向相同
8.请演算下题:质量为m=1000kg的人造卫星从位于地球赤道的卫星发射场发射到离地高为h=R0=6400km的轨道上环绕地球做匀速圆周运动.求:发射前卫星随地球自转的线速度和所需要的向心力;卫星在轨道上运行时的线速度和受到的向心力.
从演算的结果可以得出什么结论?
学生演算.演算结果:
在地面上,v0=0.465km/s;F0=33.8N;
在轨道上,v=5.585km/s;F=2450N.
在地面上,物体随地球自转的向心力F0远小于地球对物体的引力.所以,一般计算可以不考虑地球自转的影响,而认为重力等于引力.物体随地球自转的线速度v0远小于卫星在地面附近环绕地球运行的速度--第一宇宙速度(7.9km/s).
在轨道上,向心力等于引力.卫星的线速度随轨道半径的增大而减小.(动能虽然小了,势能却增大了,所以卫星在较高的轨道上运行需要有更大的机械能.)
例题分析
[例1]宇航员站在一星球表面上的某高处,沿水平方向抛出一个小球,经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L.若抛出时的初速度增大到2倍,则抛出点与落地点之间的距离为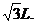 ,已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G.求该星球的质量M.
,已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G.求该星球的质量M.
分析与解:
这是一道典型的综合运用平抛运动规律和万有引力定律的题.应该注意两点:(1)“抛出点与落地点之间的距离”不是“水平射程”;
(2)“重力加速度”不是地面上的g=9.8m/s2,而应根据mg=g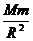 求出g=G
求出g=G 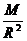 。,由于抛出点的高度不变,所以两次运动的时间相同,竖直位移均等于y=
。,由于抛出点的高度不变,所以两次运动的时间相同,竖直位移均等于y=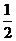 gt2;水平位移分别为x1=x和x2=2x,由平抛运动的位移公式得到
gt2;水平位移分别为x1=x和x2=2x,由平抛运动的位移公式得到
L2=x2+y2
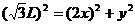
解得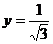
所以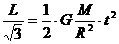
[例2]如图1-4-1所示,用细绳一端系着的质量为M=0.6kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为m=0.3kg的小球B,A的重心到O点的距离为0.2m.若A与转盘间的最大静摩擦力为f=2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(取g=10m/s2)
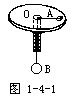
分析与解:
要使B静止,A必须相对于转盘静止--具有与转盘相同的角速度.A需要的向心力由绳拉力和静摩擦力合成.角速度取最大值时,A有离心趋势,静摩擦力指向圆心O;角速度取最小值时,A有向心运动的趋势,静摩擦力背离圆心O.
对于B,T=mg
对于A,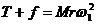 ,
,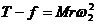
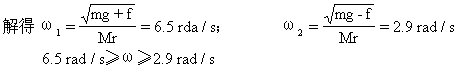
[例3]一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径与细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针运动,经过最低点时的速度都为v0.设A球运动到最低点时,B球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么m1、m2、R与v0应满足的关系式是______.
分析与解:
这是一道综合运用牛顿运动定律、圆周运动、机械能守恒定律的高考题.
A球通过圆管最低点时,圆管对球的压力竖直向上,所以球对圆管的压力竖直向下.若要此时两球作用于圆管的合力为零,B球对圆管的压力一定是竖直向上的,所以圆管对B球的压力一定是竖直向下的.
由机械能守恒定律,B球通过圆管最高点时的速度v满足方程
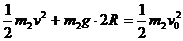 (1)
(1)
根据牛顿运动定律
对于A球
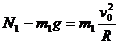 (2)
(2)
对于B球
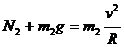 (3)
(3)
解得 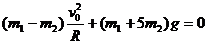
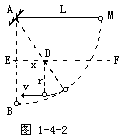
[例4]质量为m的小球,由长为l的细线系住,细线的另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=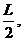 过E作水平线EF,在EF上钉一铁钉D,如图1-4-2所示.若线能承受的最大拉力是9mg,现将悬线拉至水平,然后由静止释放,若小球能绕钉子在竖直平面内做圆周运动,求钉子位置在水平线上的取值范围.不计线与钉碰撞时的能量损失.
过E作水平线EF,在EF上钉一铁钉D,如图1-4-2所示.若线能承受的最大拉力是9mg,现将悬线拉至水平,然后由静止释放,若小球能绕钉子在竖直平面内做圆周运动,求钉子位置在水平线上的取值范围.不计线与钉碰撞时的能量损失.
分析与解:
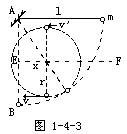
设ED=x,则细线碰到钉子后,做圆周运动的半径r=L-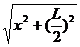 ,此半径必须满足两个临界条件
,此半径必须满足两个临界条件
小球通过该圆的最低点时,
细线拉力F≤9mg (1)
小球通过该圆的最高点时,
小球的速度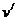 ≥
≥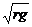 (2)
(2)
根据机械能守恒定律,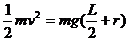 (3)
(3)
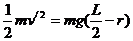 (4)
(4)
由牛顿运动定律,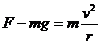 (5)
(5)
联立解(1)、(3)、(5)得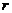 ≥
≥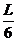 ,即
,即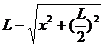 ≥
≥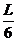 ,
,
所以x≤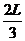
联立解(2)、(4)得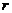 ≤
≤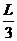 ,即
,即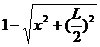 ≤
≤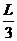 ,所以x≥
,所以x≥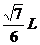
故x的取值范围是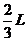 ≥x≥
≥x≥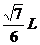
[例5]如图1-4-4所示,在XOZ(Z轴与纸面垂直)平面的上、下方,分别有磁感应强度为B1、B2的匀强磁场.已知B2=3B1,磁场方向沿Z轴指向纸外.今有一质量为m、带电量为q的带正电的粒子,自坐标原点O出发,在XOY平面(纸面)内,沿与X轴成30°方向,以初速度v0射入磁场.问:
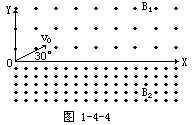
(1)粒子从O点射出到第一次通过X轴,经历的时间是多少?并确定粒子第一次通过X轴的点的坐标.
(2)粒子从O点射出到第六次通过X轴,粒子沿X轴方向的平均速度是多少?并画出粒子运动的轨迹示意图.
分析与解:
带电粒子在匀强磁场中做匀速圆周运动的圆心位置,可根据几何知识确定.
如右图1-4-5所示,粒子从O点出发,在磁场B1中顺时针绕行60°弧,第一次通过X轴的位置在X轴上的P点,圆心在O1点,半径为R1:
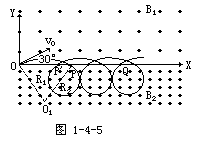
(1)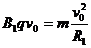 ,所以半径
,所以半径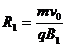 ,周期
,周期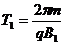 ,因为
,因为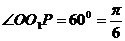 ,所以
,所以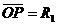 ,从O到P点的时间
,从O到P点的时间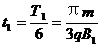
P点坐标为(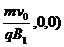
(2)粒子在磁场B2中顺时针绕行300°弧后通过X轴的位置在P/点,圆心在O2点,半径为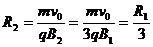 ,周期为
,周期为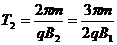
因为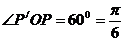 ,所以
,所以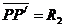 ,所以
,所以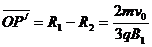
从P到P’的时间t2=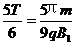
粒子第六次通过X轴的位置为Q点,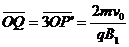
从O到Q的时间t=3(t1+t2)=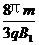
粒子从O到Q沿X轴方向的平均速度为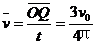
同步练习
7.问:解决天体(或人造卫星、飞船)做匀速圆周运动问题的主要依据是什么?
答:向心力由万有引力提供.即:F引=F向=man.
其中,an应根据具体情况选用不同的表达式.
6、问:公式F=G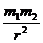 在什么情况下适用?
在什么情况下适用?
答:公式F=G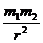 只适用于质点或质量分布均匀的球体,式中r是质点间或球心间的距离.
只适用于质点或质量分布均匀的球体,式中r是质点间或球心间的距离.
5.问:请叙述万有引力定律的内容.
答:任何两个物体之间都存在相互吸引的力.引力的大小跟两个物体质量的乘积成正比,跟它们之间距离的二次方成反比.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com