2、如图2-1所示，轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上，质量为m的物块悬挂在绳上O点，O与A、B两滑轮的距离相等。在轻绳两端C、D分别施加竖直向下的恒力F=mg。先托住物块，使绳处于水平拉直状态，由静止释放物块，在物块下落过程中，保持C、D两端的拉力F不变。

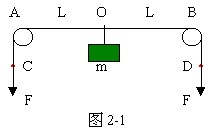
(1)当物块下落距离h为多大时，物块的加速度为零？

(2)在物块下落上述距离的过程中，克服C端恒力F做功W为多少？

(3)求物块下落过程中的最大速度Vm和最大距离H？

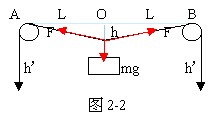
分析与解：物块向下先作加速运动，随着物块的下落，两绳间的夹角逐渐减小。因为绳子对物块的拉力大小不变，恒等于F，所以随着两绳间的夹角减小，两绳对物块拉力的合力将逐渐增大，物块所受合力逐渐减小，向下加速度逐渐减小。当物块的合外力为零时，速度达到最大值。之后，因为两绳间夹角继续减小，物块所受合外力竖直向上，且逐渐增大，物块将作加速度逐渐增大的减速运动。当物块下降速度减为零时，物块竖直下落的距离达到最大值H。

当物块的加速度为零时，由共点力平衡条件可求出相应的θ角，再由θ角求出相应的距离h，进而求出克服C端恒力F所做的功。

对物块运用动能定理可求出物块下落过程中的最大速度Vm和最大距离H。

(1)当物块所受的合外力为零时，加速度为零，此时物块下降距离为h。因为F恒等于mg，所以绳对物块拉力大小恒为mg，由平衡条件知：2θ=120°，所以θ=60°，由图2-2知：h=L*tg30°=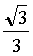L　 　 　　　 　 　　 　 [1]

(2)当物块下落h时，绳的C、D端均上升h’，由几何关系可得：h’=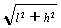-L　　 [2]

克服C端恒力F做的功为：W=F*h’ 　 　　　 　　 　　 [3]

由[1]、[2]、[3]式联立解得：W=(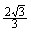-1)mgL

(3)出物块下落过程中，共有三个力对物块做功。重力做正功，两端绳子对物块的拉力做负功。两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功。因为物块下降距离h时动能最大。由动能定理得：mgh-2W=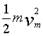　 　　　　 [4]

将[1]、[2]、[3]式代入[4]式解得：Vm=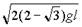

当物块速度减小为零时，物块下落距离达到最大值H，绳C、D上升的距离为H’。由动能定理得：mgH-2mgH’=0，又H’=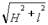-L，联立解得：H=。

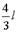1、如图1-1所示，长为5米的细绳的两端分别系于竖立在地面上相距为4米的两杆顶端A、B。绳上挂一个光滑的轻质挂钩。它钩着一个重为12牛的物体。平衡时，绳中张力T=＿＿＿＿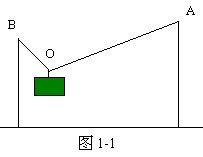

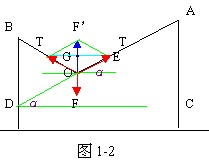
分析与解：本题为三力平衡问题。其基本思路为：选对象、分析力、画力图、列方程。对平衡问题，根据题目所给条件，往往可采用不同的方法，如正交分解法、相似三角形等。所以，本题有多种解法。

解法一：选挂钩为研究对象，其受力如图1-2所示

设细绳与水平夹角为α，由平衡条件可知：2TSinα=F，其中F=12牛

将绳延长，由图中几何条件得：Sinα=3/5，则代入上式可得T=10牛。

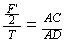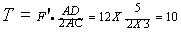解法二：挂钩受三个力，由平衡条件可知：两个拉力(大小相等均为T)的合力F’与F大小相等方向相反。以两个拉力为邻边所作的平行四边形为菱形。如图1-2所示，其中力的三角形△OEG与△ADC相似，则： 得：牛。

想一想：若将右端绳A 沿杆适当下移些，细绳上张力是否变化？

(提示：挂钩在细绳上移到一个新位置，挂钩两边细绳与水平方向夹角仍相等，细绳的张力仍不变。)

(一)、直流电路　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

1、电流强度的定义：　　　 I = 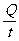　　　　　　(I=nesv)　

2、电阻定律：( 只与导体材料性质和温度有关，与导体横截面积和长度无关)　

3、电阻串联、并联：

　　　　　　 串联：R=R₁+R₂+R₃ +……+R_n

 并联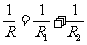：　 　　　　　两个电阻并联：　 R=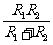

4、欧姆定律：(1)、部分电路欧姆定律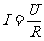：　　 U=IR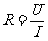　　

　　　　　　　 (2)、闭合电路欧姆定律：I =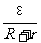　　　　　　 ε　 r

　　　　　　　　　　　 路端电压：　　 U = e －I r= IR　　　　　　 R　　　

　　　　　　　　　　　 输出功率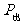：　　 　= Iε－I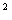r =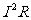

　　　　　　　　　　　 电源热功率：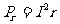　 　　　　

　　　　　　　　　　　 电源效率：　　　 = =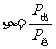　　

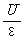　　　　 (5)．电功和电功率：　　　　 电功：W=IUt　　　　 电热：Q=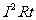　

　　　　　　　　　　　　　　　　 电功率 ：P=IU

　　　　　 对于纯电阻电路：　　 W=IUt=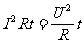　　 P=IU =(　 )

　　　　　 对于非纯电阻电路：　 W=IUt >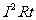　　　　　 P=IU>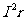　

(6)　 电池组的串联每节电池电动势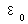为`内阻为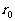，n节电池串联时

　　　　　　　 电动势：ε=n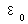　　 内阻：r=n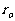

伏安法测电阻：

4、 理想气体三个实验定律：

　 (1) 玻马-定律：m一定，T不变　　　　　　　　　　　 　　　　　　　

　　　　　　　　　　 P₁V₁ = P₂V₂　 或 PV = 恒量

　 (2)查里定律：　　 m一定，V不变　　

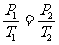　　　　　　　　 　或　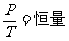 　或 P_t = P₀ (1+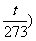　　　　　　

　 (3) 盖·吕萨克定律：m一定，T不变　　　　　　　　　　　　

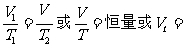　 　　　　　　　V₀ (1+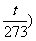　　　　

　　 注意：计算时公式两边T必须统一为热力学单位，其它两边单位相同即可。

1、热力学第一定律：　 W + Q = DE

　 符号法则： 体积增大,气体对外做功,W为“一”；体积减小,外界对气体做功,W为“+”。

　　　　　　 气体从外界吸热,Q为“+”；气体对外界放热,Q为“-”。

　　　　　　 温度升高,内能增量DE是取“+”；温度降低,内能减少，DE取“一”。

三种特殊情况： (1) 等温变化　 DE=0， 即 W+Q=0

　　　　　　　 (2) 绝热膨胀或压缩：Q=0即 W=DE

　　　　　　 　(3)等容变化：W=0 ，Q=DE　　　　　　　

2　 理想气体状态方程：　

　　　 (1)适用条件：一定质量的理想气体，三个状态参量同时发生变化。

　　　 (2)　 公式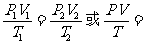：　　 恒量

　　　 (3)　 含密度式：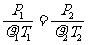

*3、 克拉白龙方程：　 PV=n RT=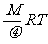　 (R为普适气体恒量，n为摩尔数)

24、 波长、波速、频率的关系： V=l f =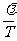　　 (适用于一切波)　

14、匀速圆周运动公式

　　　 线速度:　 V= wR=2f R=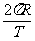　　　　　 角速度：w=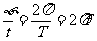

　　　 向心加速度：a =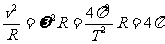² f² R　　　　　　

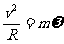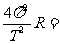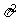　 向心力：　　　 F= ma = m² R= mm4n² R　　 　　　　　　　　　　

　 注意：(1)匀速圆周运动的物体的向心力就是物体所受的合外力，总是指向圆心。　

　　　　 (2)卫星绕地球、行星绕太阳作匀速圆周运动的向心力由万有引力提供。　　　　　　　　　　　　　　

(3)　　 氢原子核外电子绕原子核作匀速圆周运动的向心力由原子核对核外电子的库仑力提供。

　15　 直线运动公式：匀速直线运动和初速度为零的匀加速直线运动的合运动

　　　 水平分运动：　　　 水平位移： x= v_o t　　　 水平分速度：v_x = v_o

竖直分运动：　　　 竖直位移： y =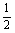g t²　　 竖直分速度：v_y= g t　　　　　　

　tgq = 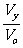　　　　　V_y = V_otgq V_o =V_yctgq

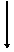
V = 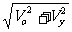　　　V_o = Vcosq　　 V_y = Vsinq　 y　　 ^V_o　　　　　

 在V_o、V_y、V、X、y、t、q七个物理量中，如果 x_{) q} v_o

　　 已知其中任意两个，可根据以上公式求出其它五个物理量。 v_y v

　 16 动量和冲量：　　　　 动量： P = mV　　　　 冲量：I = F t

　 17 动量定理：　 物体所受合外力的冲量等于它的动量的变化。

　　　　 公式： F_合t = mv^’ 一mv　　　 (解题时受力分析和正方向的规定是关键)

　 18 动量守恒定律：相互作用的物体系统，如果不受外力，或它们所受的外力之和为零，它们的总动量保持不变。　 (研究对象：相互作用的两个物体或多个物体)

　　　 公式：m₁v₁　 + m₂v₂ = m₁ v₁^‘+ m₂v₂’或Dp₁ =一Dp₂ 或Dp₁ +Dp₂=O

　适用条件：

　 (1)系统不受外力作用。　 (2)系统受外力作用，但合外力为零。

　 (3)系统受外力作用，合外力也不为零，但合外力远小于物体间的相互作用力。

　 (4)系统在某一个方向的合外力为零，在这个方向的动量守恒。

18 功 ：　　　 W = Fs cosq　　　 (适用于恒力的功的计算)

(1) 　　 理解正功、零功、负功　　

　　　 (2)　 功是能量转化的量度

　　　　　　　 重力的功------量度------重力势能的变化

　　　　　　　 电场力的功-----量度------电势能的变化

　　　　　　　 分子力的功-----量度------分子势能的变化　　　　　

　　　　　　　 合外力的功------量度-------动能的变化

19　 动能和势能：　 动能： E_k =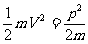 　　　

　　　　　　　　　 重力势能：E_p = mgh　　 (与零势能面的选择有关)

　20　 动能定理：外力对物体所做的总功等于物体动能的变化(增量)。

　　 公式：　 W_合= DE_k = E_k2 一E_k1 =　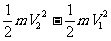 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　21　 机械能守恒定律：机械能 = 动能+重力势能+弹性势能

　　 　条件：系统只有内部的重力或弹力做功.

　　 公式：　 mgh₁ +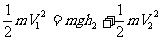　 或者　 DE_p减 = DE_k增

22　 功率：　　 P = 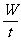　　(在t时间内力对物体做功的平均功率)

　　　 　　P = FV　　 (F为牵引力，不是合外力；V为即时速度时，P为即时功率；V为平均速度时，P为平均功率； P一定时，F与V成正比)

23 简谐振动：　　 回复力：　 F = 一KX　　　 加速度：a = 一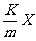

　　　　　　　　 单摆周期公式：　 T= 2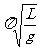　　 (与摆球质量、振幅无关)

　　　　　　　 *弹簧振子周期公式：T= 2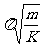　 (与振子质量有关、与振幅无关)

13、　 竖直上抛运动：　 上升过程是匀减速直线运动，下落过程是匀加速直线运动。全过程是初速度为V_O、加速度为-g的匀减速直线运动。

(1) 　　 上升最大高度： H =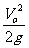

　　　 (2)　 上升的时间： t=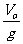

　　　 (3)　 上升、下落经过同一位置时的加速度相同，而速度等值反向

　 (4)　 上升、下落经过同一段位移的时间相等。　　　　　　　　　　

从抛出到落回原位置的时间：t =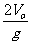 　　　

(6)　 适用全过程的公式： S = V_o t 一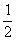g t²　　　　　 V_t = V_o一g t　　　　

　　　　　　　　　　　　 V_t² 一V_o² = 一2 gS　　 ( S、V_t的正、负号的理解)　　　

12、匀变速直线运动：

　　 基本规律：　　　 V_t = V₀ + a t　　 S = v_o t +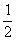a t²几个重要推论：

　 (1)　 V_t² 　－ V₀² = 2as　 (匀加速直线运动：a为正值　 匀减速直线运动：a为正值)

(2)　 A B段中间时刻的即时速度:　　　　　　　

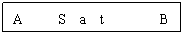　　　　 V_{t/ 2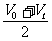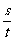} ==　　　　　　　　　　　　 (3)　 AB段位移中点的即时速度:　　　　　　　　　　　　

　　　　 V_s/2 =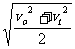 　　

　　　 匀速：V_t/2 =V_s/2　 ; 匀加速或匀减速直线运动：V_t/2 <V_s/2

(4) 　　 初速为零的匀加速直线运动,在1s 、2s、3s­……ns内的位移之比为1²：2²:3²

……n²；　 在第1s 内、第 2s内、第3s内……第ns内的位移之比为1：3：5……

(2n-1);　 在第1米内、第2米内、第3米内……第n米内的时间之比为1：：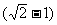

……(

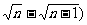
(5) 　　 初速无论是否为零,匀变速直线运动的质点,在连续相邻的相等的时间间隔内的位移之差为一常数：Ds = aT² 　　(a一匀变速直线运动的加速度　 T一每个时间间隔的时间)　

11、 牛顿第二定律：　　 F_合 = ma　 或者 åF_x = m a_x　　 åF_y = m a_y

理解：(1)矢量性　 (2)瞬时性　 (3)独立性　

(4) 同体性　 (5)同系性　 (6)同单位制