
题目列表(包括答案和解析)
23.(本小题满分8分)
如图13-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图13-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;

 (2)若三角尺GEF旋转到如图13-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
(2)若三角尺GEF旋转到如图13-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.


22.(本小题满分8分)
 探索
探索
在如图12-1至图12-3中,△ABC的面积为a .
(1)如图12-1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示);
 (2)如图12-2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含a的代数式表示),并写出理由;
(2)如图12-2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含a的代数式表示),并写出理由;

(3)在图12-2的基础上延长AB到点F,使BF=AB,连结FD,
FE,得到△DEF(如图12-3).若阴影部分的面积为S3,
则S3=__________(用含a的代数式表示).
发现
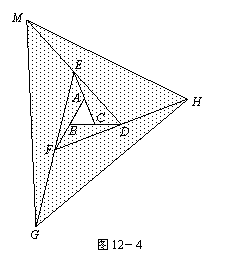 像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图12-3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_______倍.
像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图12-3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_______倍.
应用
去年在面积为10m2的△ABC空地上栽种了某种花卉.今年准备扩大种植规模,把△ABC向外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH(如图12-4).求这两次扩展的区域(即阴影部分)面积共为多少m2?

21.(本小题满分8分)
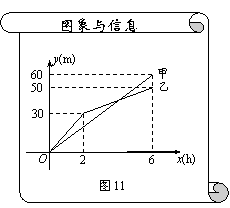
甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图11所示,请根据图象所提供的信息解答下列问题:
(1)乙队开挖到30m时,用了_____h.开挖6h
时甲队比乙队多挖了_____m;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函
数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)当x为何值时,甲、乙两队在施工过程中所挖河渠的长度相等?

20.(本小题满分8分)
某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
|
员工 |
管理人员 |
普通工作人员 |
|||||
|
人员结构 |
总经理 |
部门经理 |
科研人员 |
销售人员 |
高级技工 |
中级技工 |
勤杂工 |
|
员工数/名 |
1 |
3 |
2 |
3 |
 |
24 |
1 |
|
每人月工资/元 |
21000 |
8400 |
2025 |
2200 |
1800 |
1600 |
950 |
 请你根据上述内容,解答下列问题:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数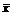 为2500元,
为2500元,
中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.
请你回答右图中小张的问题,并指
出用(2)中的哪个数据向小张介绍
员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资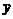 (结果保留整数),并判断
(结果保留整数),并判断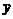 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.
19.(本小题满分8分)
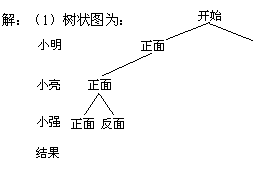
小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如右图:
(1)请你完成下面表示游戏一个回合所有可能出现
的结果的树状图;
(2)求一个回合能确定两人先下棋的概率.

18.(本小题满分7分)
观察下面的点阵图形和与之相对应的等式,探究其中的规律:
(1)请你在④和⑤后面的横线上分别写出相对应的等式:
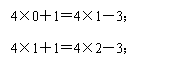 |
|||||||||
|
|||||||||
 |
|||||||||
 |
|||||||||
|
|||||||||
 |
|||||||||
 |
|||||||||
 |
|
||||||
|
|||||||
 |
|||||||
 |
|||||||
|
|
||||||
 |
|||||||
 |
|||||
|
|||||
 |
|||||
|
|||
|
|||
(2)通过猜想,写出与第n个图形相对应的等式.


17.(本小题满分7分)
如图10所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图10中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知:MN=20 m,MD=8 m,PN=24 m,求(1)中的点C到胜利街口的距离CM.


16.(本小题满分7分)
已知x =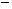
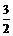 ,求(1+
,求(1+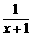 )
) (x+1)的值.
(x+1)的值.
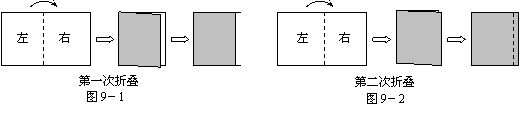
15.小宇同学在一次手工制作活动中,先把一张矩形纸片按图9-1的方式进行折叠,使折痕的左侧部分比右侧部分短1cm;展开后按图9-2的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm,再展开后,在纸上形成的两条折痕之间的距离
是_______cm.
14.如图8,PA是⊙O的切线,切点为A,PA=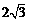 ,∠APO=30°,则⊙O的半径长为_______.
,∠APO=30°,则⊙O的半径长为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com