
题目列表(包括答案和解析)
21.(本小题满分14分)设函数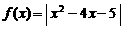 .
.
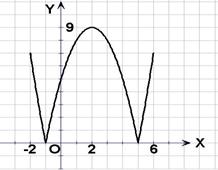
(Ⅰ)在区间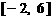 上画出函数
上画出函数 的图像;
的图像;
(Ⅱ)设集合 . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明;
之间的关系,并给出证明;
(Ⅲ)当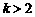 时,求证:在区间
时,求证:在区间 上,
上,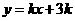 的图像位于函数
的图像位于函数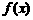 图像的上方
图像的上方
解:(Ⅰ)
(Ⅱ)方程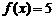 的解分别是
的解分别是 和
和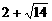 ,由于
,由于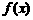 在
在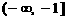 和
和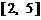 上单调递减,在
上单调递减,在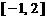 和
和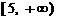 上单调递增,因此
上单调递增,因此
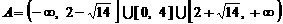 .
.
由于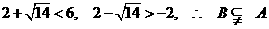 .
.
(Ⅲ)[解法一] 当 时,
时, .
.
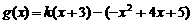
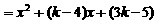
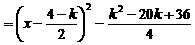 ,
,
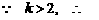
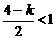 . 又
. 又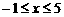 ,
,
①
当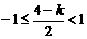 ,即
,即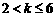 时,取
时,取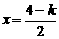 ,
,

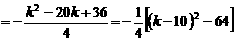 .
.
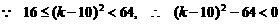 ,
,
则 .
.
②
当 ,即
,即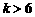 时,取
时,取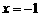 ,
,  =
=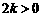 .
.
由 ①、②可知,当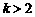 时,
时,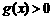 ,
, .
.
因此,在区间 上,
上,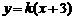 的图像位于函数
的图像位于函数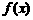 图像的上方.
图像的上方.
[解法二] 当 时,
时, .
.
由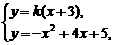 得
得 ,
,
令 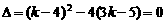 ,解得
,解得 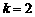 或
或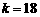 ,
,
在区间 上,当
上,当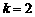 时,
时,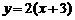 的图像与函数
的图像与函数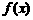 的图像只交于一点
的图像只交于一点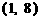 ;
;
当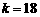 时,
时, 的图像与函数
的图像与函数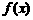 的图像没有交点.
的图像没有交点.
如图可知,由于直线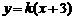 过点
过点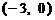 ,当
,当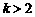 时,直线
时,直线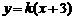 是由直线
是由直线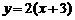 绕点
绕点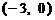 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间 上,
上,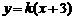 的图像位于函数
的图像位于函数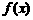 图像的上方.
图像的上方.
20.(本小题满分14分)已知:定义在R上的函数f (x)为奇函数,且在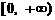 上是增函数.
上是增函数.
(Ⅰ)求证:f (x)在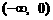 上也是增函数;
上也是增函数;
(Ⅱ)对任意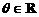 ,求实数m的取值范围,使不等式
,求实数m的取值范围,使不等式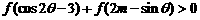 恒成立.
恒成立.
解:(Ⅰ)证明:设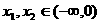 ,且
,且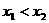 ,
,
则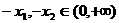 ,且
,且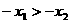 .
.
∵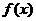 在
在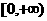 上是增函数,∴
上是增函数,∴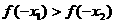 .
.
又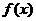 为奇函数,∴
为奇函数,∴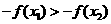 ,
,
∴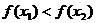 , 即
, 即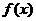 在
在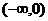 上也是增函数.
上也是增函数.
(Ⅱ)∵函数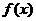 在
在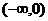 和
和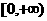 上是增函数,且
上是增函数,且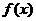 在R上是奇函数,
在R上是奇函数,
∴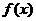 在
在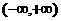 上是增函数.
上是增函数.
于是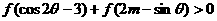





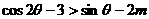

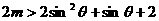

 .
.
∵当 时,
时,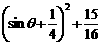 的最大值为
的最大值为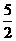 ,∴当
,∴当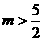 时,不等式恒成立.
时,不等式恒成立.
19.(本小题满分14分)设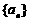 为公差大于0的等差数列,
为公差大于0的等差数列,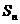 为数列
为数列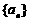 的前n项的和.
的前n项的和.
已知S4=24,
(Ⅰ)求数列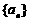 的通项公式
的通项公式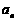 ;
;
(Ⅱ)若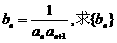 的前n项和
的前n项和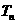
解:(Ⅰ)
由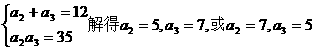
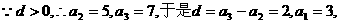
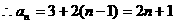
(Ⅱ)
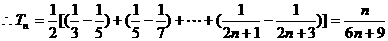
18.(本小题满分16分)已知函数 .
.
(Ⅰ)求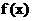 的最小正周期及递减区间;
的最小正周期及递减区间;
(Ⅱ)指出将函数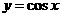 的图象经过怎样的变换而得到函数
的图象经过怎样的变换而得到函数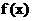 的图象;
的图象;
(Ⅲ)若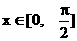 , 求
, 求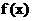 最大值、最小值.
最大值、最小值.
解:(Ⅰ)
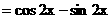
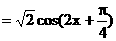 ∴
∴ 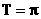
递减区间
(Ⅱ)先把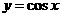 各点的横坐标缩小到原来的
各点的横坐标缩小到原来的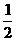 (纵坐标不变),再向左平移
(纵坐标不变),再向左平移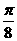 个单位,再把纵坐标扩大到原来的
个单位,再把纵坐标扩大到原来的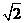 倍(横坐标不变)而得到函数
倍(横坐标不变)而得到函数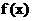 的图象
的图象
(Ⅲ)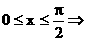
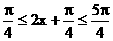
当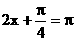 即
即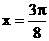 时
时 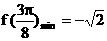
当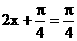 即
即 时
时 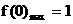
17.(本小题满分12分)有四个正数 ,前三数成等比数列,其和为
,前三数成等比数列,其和为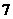 ;后三数成等差数列,其和为
;后三数成等差数列,其和为 .
.
(Ⅰ)求此四数;
(Ⅱ)分别求以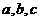 为前三项的等比数列的前
为前三项的等比数列的前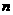 项和
项和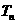 与以
与以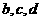 为前三项的等差数列的
为前三项的等差数列的
前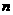 项和
项和 ;
;
(Ⅲ)比较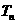 与
与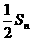 的大小.
的大小.
解:(Ⅰ)依题意有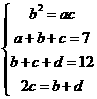
解得四数依次为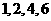 或
或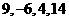 ,因为四数均为正数。所以所求四数依次为
,因为四数均为正数。所以所求四数依次为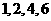
(Ⅱ)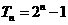 ,
,
(Ⅲ)当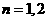 时,
时,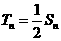
当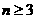 时,
时,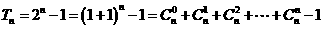

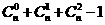
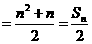
16.给出下列四个函数:①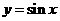 ;②
;②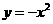 ;③
;③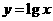 ;④
;④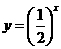 ,对于其定义域内的任意的
,对于其定义域内的任意的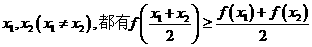 成立的函数为 ②③
成立的函数为 ②③
15.定义运算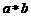 为:
为: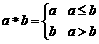 ,例如,
,例如,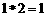 ,则函数
,则函数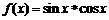 的值域[-1,
的值域[-1,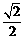 ]
]
14.已知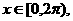 且
且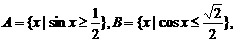 则A∩B=
则A∩B= 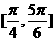
13.已知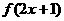 是偶函数,则函数
是偶函数,则函数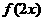 的图象的对称轴是
的图象的对称轴是 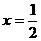
12.一条信息,若一人得知后,一小时内将信息传给两人,这两人又在一小时内各传给未知信息的另外两人.如此下去,要传遍55人的班级所需时间大约为__5_____小时.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com