
题目列表(包括答案和解析)
3.设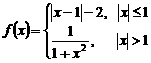 ,则f[f(
,则f[f(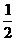 )]=(
)
)]=(
)
A .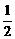 B.
B. 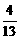 C.
C. 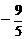 D.
D. 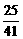
2.已知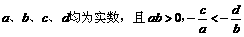 ,则下列不等式中成立的是
,则下列不等式中成立的是
A.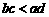 B.
B.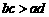 C.
C.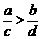 D.
D.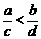
1.已知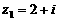 ,
,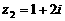 ,则复数
,则复数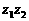 在复平面内所对应的点位于( )
在复平面内所对应的点位于( )
A. 第一象限 B. 第二象限; C. 虚轴的正向 D. 虚轴的负向.
21. ∵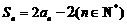 ,∴
,∴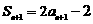 ,
,
于是an+1=Sn+1-Sn=(2 an+1-2)-(2 an-2),即an+1=2an. …………2分
又a1=S1=2 a1-2, 得a1=2. …………1分
∴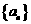 是首项和公比都是2的等比数列,故an=2n.
…………1分
是首项和公比都是2的等比数列,故an=2n.
…………1分
(2) 由a1b1=(2×1-1)×21+1+2=6及a1=2得b1=3. …………1分
当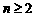 时,
时,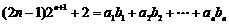
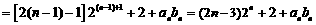 ,
,
∴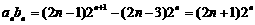 .
…………2分
.
…………2分
∵an=2n,∴bn=2n+1(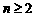 ).
).
∴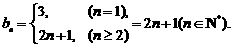
(3)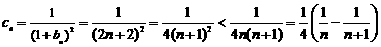 .
.
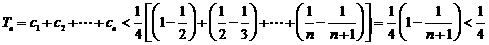 .
.
20.解: (1)由已知, 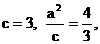 ∴
∴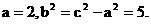
所以求双曲线C的方程为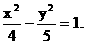 …………(4分)
…………(4分)
(2)设P的坐标为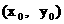 , M, N的纵坐标分别为
, M, N的纵坐标分别为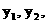 …………(5分)
…………(5分)
∵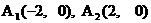 , ∴
, ∴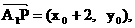
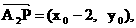
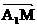
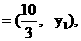
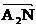
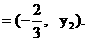 …………(6分)
…………(6分)
∵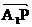 与
与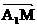 共线, ∴
共线, ∴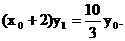
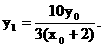
同理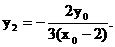 …………(8分)
…………(8分)
∵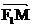
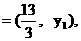
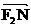
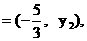
∴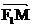 ·
·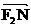 =
=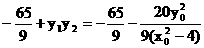 …………(10分)
…………(10分)
=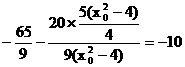 …………(12分)
…………(12分)
19.(1)设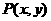 ,由
,由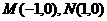 ,得
,得
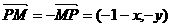 ,
,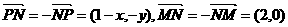
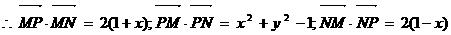 ,
, 3分
3分
于是,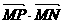 ,
,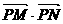 ,
,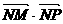 成等差数列等价于
成等差数列等价于
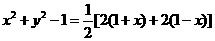
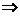
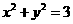
 6分
6分
所以点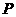 的轨迹是以原点为圆心,
的轨迹是以原点为圆心, 为半径的圆;
为半径的圆;
 7分
7分
(2)设直线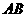 的方程为
的方程为 ,
,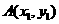 、
、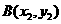 ,
,
 直线
直线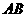 与曲线
与曲线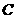 相切,
相切,
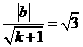 ,即
,即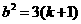
 ①,
①,  9分
9分
由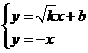
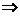
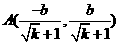 ,同理
,同理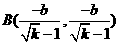 ,
,
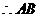 的中点
的中点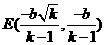 ,
,
 10分
10分

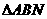 是以
是以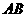 为底边的等腰三角形,
为底边的等腰三角形,
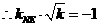 ,即
,即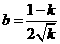
 ②,
②,
 12分
12分
由①②解得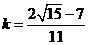 .
.
 14分
14分
18.
(1)∵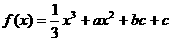
∴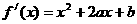 ……………………………………………………… … 2分
……………………………………………………… … 2分
又∵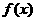 在
在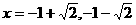 处取得极值
处取得极值
∴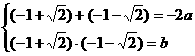 ……………………………………………… 4分
……………………………………………… 4分
解得 a = 1,b = ―1……………………………………………………………… 5分
(2)不等式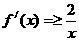
即 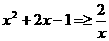
等价于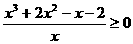 ……………………………………………………… 7分
……………………………………………………… 7分
即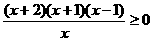 ……………………………………………………… 9分
……………………………………………………… 9分
所以原不等式解集为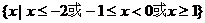 ………………………… 12分
………………………… 12分
17.(本小题共12分)在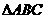 中,角
中,角 、
、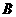 、
、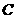 所对的边是
所对的边是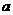 、
、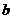 、
、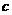 ,且
,且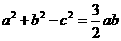 .
.
(1)求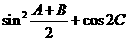 值 ;
值 ;
(2)若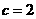 ,求
,求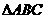 面积的最大值.
面积的最大值.
(1)
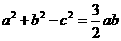 ,
,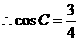 ,
,
 2分
2分
由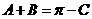 ,
,
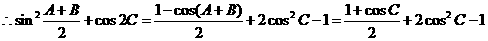
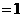 ;
; 6分
6分
(2)
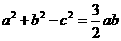 ,且
,且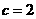 ,
,
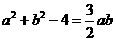 ,
,
又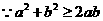 ,
,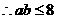 ,
,
 9分
9分
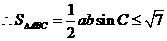 .
.
 11分
11分
当切仅当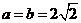 时,
时,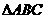 面积取最大值,最大值为
面积取最大值,最大值为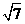 .
.  12分
12分
15.
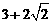 16.
16. 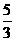
11.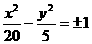 12.
12.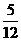 13.
13. 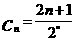 14.3或13
14.3或13
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com