
题目列表(包括答案和解析)
21.[解](1)由题意, ,
,
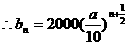 …(4分)
…(4分)
[解](2)∵函数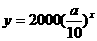 递减,
递减,
∴对每个自然数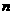 ,有
,有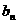 >
>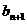 >
>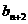 ,
,
则以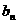 ,
,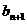 ,
,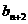 为边长能构成一个三角形的充要条件是
为边长能构成一个三角形的充要条件是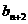 +
+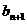 >
>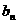 ,
,
即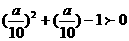 ,
…(7分)
,
…(7分)
解得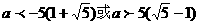 ,
,
∴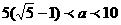 …(10分)
…(10分)
[解](3)∵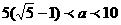 ,
,
∴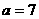 ,
,
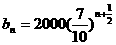 ,
…(12分)
,
…(12分)
于是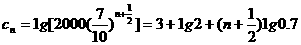 ,
,
数列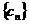 是一个递减的等差数列。
是一个递减的等差数列。
因此,当且仅当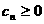 ,且
,且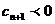 时,数列
时,数列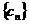 的前
的前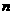 项的和最大。
项的和最大。
由 ,
,
得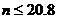 ,
,
∴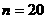 …(16分)
…(16分)
20.[解](1)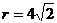 ,
,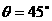 ,
,
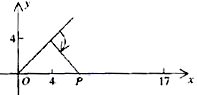 得指令为
得指令为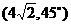 ,
…(4分)
,
…(4分)
(2)设机器人最快在点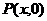 处截住小球…(6分)
处截住小球…(6分)
则因为小球速度是机器人速度的2倍,所以在相同时间内有
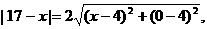 …(8分)
…(8分)
即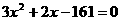
得 。
。
∵要求机器人最快地去截住小球,即小球滚动距离最短,
∴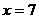
故机器人最快可在点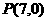 处截住小球,
…(10分)
处截住小球,
…(10分)
所给的指令为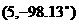 …(14分)
…(14分)
19.[解](1)当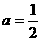 时,
时,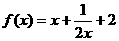 ,
,
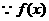 在区间[
在区间[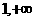 ]上为增函数,
…(3分)
]上为增函数,
…(3分)
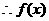 在区间[
在区间[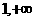 ]上的最小值为
]上的最小值为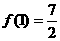 …(6分)
…(6分)
(2)[解法一]在区间的[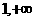 ]上,
]上,
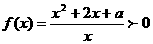 的恒成立
的恒成立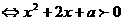 恒成立,
…(8分)
恒成立,
…(8分)
设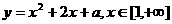 ,
,
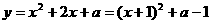 递增,∴当
递增,∴当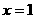 时,
时,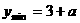 , …(12分)
, …(12分)
于是当且仅当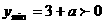 时,函数
时,函数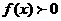 恒成立,
恒成立,
故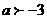 …(14分)
…(14分)
(2)[解法二]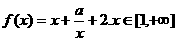 ,
,
当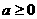 时,函数
时,函数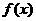 的值恒为正,
…(8分)
的值恒为正,
…(8分)
当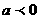 时,函数
时,函数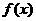 递增,
递增,
故当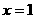 时,
时, ,
…(12分)
,
…(12分)
于是当且仅当 时,
时,
函数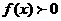 恒成立,
恒成立,
故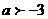 …(14分)
…(14分)
18.[解法一]如图建立空间直角坐标系, …(2分)
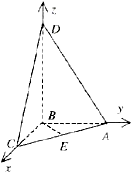 由题意,有
由题意,有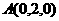 ,
,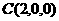 ,
,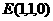
设D点的坐标为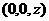
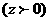 ,
,
则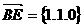 ,
,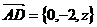 …(6分)
…(6分)
则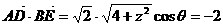 ,
,
且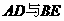 所成的角的大小为
所成的角的大小为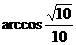 。
。
∴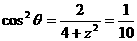 ,
,
得 ,故BD的长度是4, …(10分)
,故BD的长度是4, …(10分)
又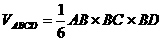 ,
,
因此四面体ABCD的体积是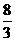 ,
…(12分)
,
…(12分)
[解法二]过A引BE的平行线,交CB的延长线于F,∠DAF是异面直线BE与AD所成的角。
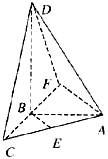 ∴∠DAF=
∴∠DAF=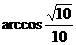 ,
…(4分)
,
…(4分)
∵E是AC的中点,∴B是CF的中点,
AF=2BE=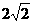 。
…(6分)
。
…(6分)
又BF,BA分别是DF,DA的射影,且BF=BC=BA,
∴DF=DA …(8分)
三角形ADF是等腰三角形,
AD=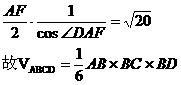 ,
…(10分)
,
…(10分)
因此四面体ABCD的体积是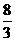 …(12分)
…(12分)
17.[解]设椭圆C的方程为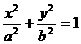 …(2分)
…(2分)
由题意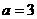 ,
, ,于是
,于是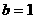 。
。
∴椭圆C的方程为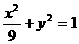 …(4分)
…(4分)
由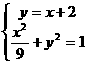 得
得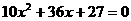
因为该二次方程的判别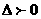 ,所以直线与椭圆有两个不同交点。 …(8分)
,所以直线与椭圆有两个不同交点。 …(8分)
设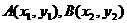
则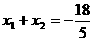 ,
,
故线段AB的中点坐标为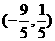 …(12分)
…(12分)
12.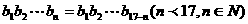
9.-462 10.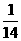 11.(0,5)
11.(0,5)
5.1 6.9 7.侧棱相等/侧棱与底面所成角相等/…… 8.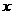
1.4 2.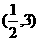 3.(-4,0),(6,0)
4.
3.(-4,0),(6,0)
4.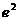
3.第17题至第22题中左端所注的分数,表示考生正确做到这一步应得的该题的累加分数。给分或扣分均以1分为单位。
解答
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com