
题目列表(包括答案和解析)
1.已知集合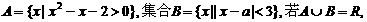 ,则实数a的取值
,则实数a的取值
范围是 ( )
A.[1,2] B.(-1,2) C.[-1,2] D.(-2,1)
22.(本小题满分14分)
已知二次函数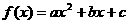 满足以下条件:
满足以下条件:
①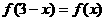 ;
;
②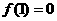 ;
;
③对任意实数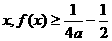 恒成立.
恒成立.
(1)求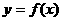 的表达式;
的表达式;
(2)数列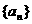 、
、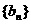 ,若对任意的实数
,若对任意的实数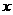 都满足
都满足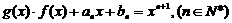
其中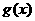 是定义在实数集R上的一个函数.求数
是定义在实数集R上的一个函数.求数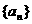 与
与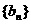 的通项公式;
的通项公式;
(3)设圆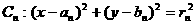 ,若圆
,若圆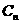 现圆
现圆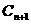 外切,
外切,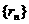 是各项都是正
是各项都是正
数且公比为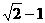 的等比数列.求
的等比数列.求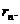
解:(1)由条件得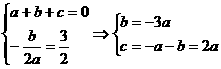
由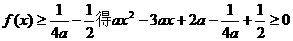 恒成立
恒成立
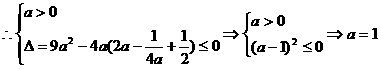
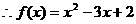
(2)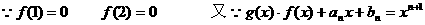 恒成立
恒成立
令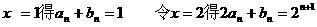 ……7分
……7分
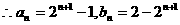 ……10分
……10分
(3)
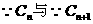 相外切
相外切 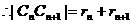 ……11分
……11分
而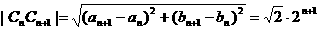
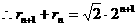 即
即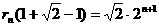
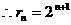
21.(本小题满分14分)
(理科)已知椭圆C的中心在原点,焦点在x轴上,一条经过点(3,-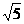 )且方向向量为
)且方向向量为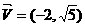 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又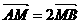 .
.
(1) 求直线l方程; (2)求椭圆C长轴长取值的范围.
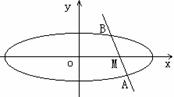 解:(1)直线l过点(3,-
解:(1)直线l过点(3,-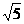 )且方向向量为
)且方向向量为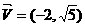
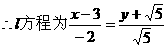 化简为:
化简为: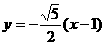
(2)设直线
交于两点A(x1,y1),B(x2,y2),和x轴交于M(1,0)
由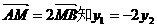
将
由韦达定理知: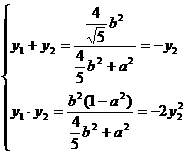 由②2/③
知:32b2=(4b2+5a2)(a2-1)
由②2/③
知:32b2=(4b2+5a2)(a2-1)
化为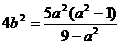 对方程①求判别式,且由△>0
对方程①求判别式,且由△>0
即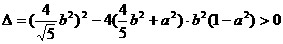 化简为:
化简为: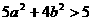
由④式代入⑤可知: 又椭圆的焦点在x轴上,
又椭圆的焦点在x轴上,
则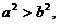 由④知:
由④知: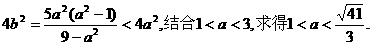
因此所求椭圆长轴长2a范围为(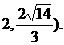
20.(本小题满分12分)
函数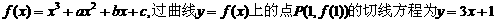
(1)若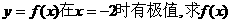 的表达式;
的表达式;
(2)若函数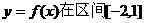 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.

(2)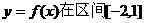 上单调递增又
上单调递增又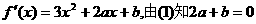
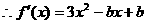
依题意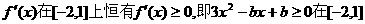 上恒成立.
上恒成立.
①在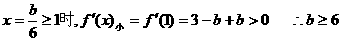
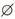 ②在
②在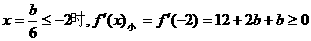
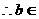
③在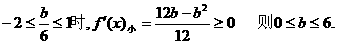
综合上述讨论可知,所求参数b取值范围是:b≥0
19.数列{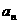 }满足递推式
}满足递推式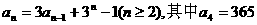
(1)求a1,a2,a3;
(2)若存在一个实数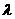 ,使得
,使得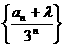 为等差数列,求
为等差数列,求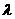 值;
值;
(3)求数列{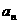 }的前n项之和.
}的前n项之和.
解:(1)由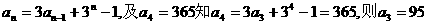
同理求得a2=23, a1=5


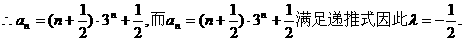
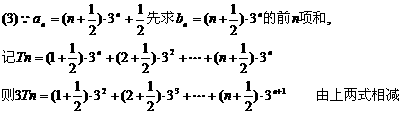
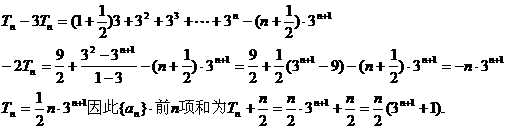
18.(本小题满分12分)
 在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(1)求DP和平面ABCD所成的角的正切;
(2)求四面体P-AC′D′的体积;
(3)求DP和AC′所成角.
解:(1)过P作PH⊥BC于足H,连DH,
∵面BC′⊥面AC,则PH⊥面ABCD,
∴DP和面ABCD所成角即为∠HDP.
在正方形BCC′B′,M,N分别为BB′,B′C′中点,P为MN中点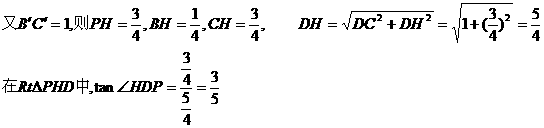
(2)连BC′和B′C交于Q,因为BCC′B′为正方形,则PQ⊥BC′
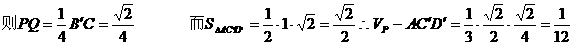 (3)延长BC至E,延长
(3)延长BC至E,延长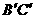 至F,使CE=C′F=1,连DF,则DF//AC′
至F,使CE=C′F=1,连DF,则DF//AC′
∴异面直线AC′和DP所成角转化为求∠PDF,连PF
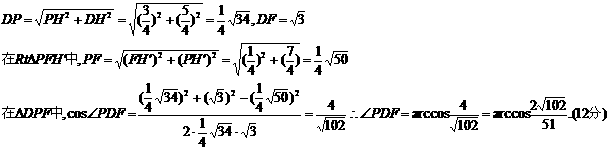
17.(本小题满分12分)若锐角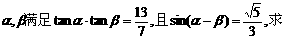
(1)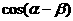 ; (2)
; (2)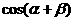
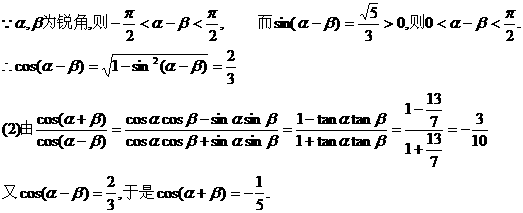
16.给出下列四个命题,①若f(x+2)=f(2-x),则f(x)的图象关于x=2对称,②若f(x+2)=f(2-x),则f(x)的图象关于y轴对称。③函数y=f(2+x)与y=f(2-x)的图象关于x=2对称。④函数y=f(2+x)与y=f(2-x)的图象关于y轴对称。正确的命题是①④
15.定义符号函数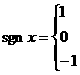
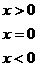 ,则不等式
,则不等式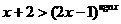 的解集是
的解集是
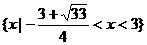
14.某气象站天气预报准确率是80%,5次预报中至少有4次准确的概率是: 0.74
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com