
题目列表(包括答案和解析)
5、确定事件(分为必然事件、不可能事件)、不确定事件(称为随机事件或可能事件)、概率。并能用树状图和列表法计算概率;
例12:下列事件中,属于必然事件的是( )
A、明天我市下雨 B、抛一枚硬币,正面朝上
C、我走出校门,看到的第一辆汽车的牌照的末位数字是偶数
D、一口袋中装有2个红球和1个白球,从中摸出2个球,其中有红球
例13:用列表的方法求下列概率:已知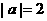 ,
,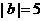 .求
.求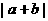 的值为7的概率.
的值为7的概率.
例14:画树状图或列表求下列的概率:袋中有红、黄、白色球各一个,它们除颜色外其余都相同,任取一个,放回后再任取一个.画树状图或列表求下列事件的概率.
(1)都是红色 (2)颜色相同 (3)没有白色
4、频数,频率,频率分布,常用的统计图表。
例9:第十中学教研组有25名教师,将他的年龄分成3组,在38-45岁组内有8名教师,那么这个小组的频率是( )
 (A)0.12 (B)0.38
(C)0.32 (D)3.12
(A)0.12 (B)0.38
(C)0.32 (D)3.12
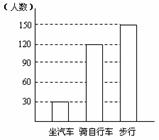
例10:如图是某校初一年学生到校方式的条形统计图,根据图形可得出步行人数占总人数的( )
A.60%; B.50%;
C.30%; D.20%.
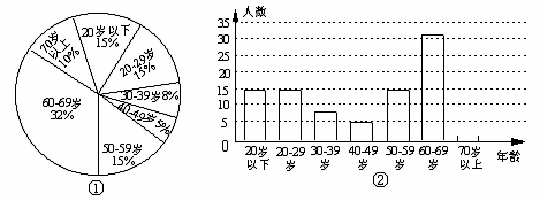 例11:在市政府举办的“迎奥运登山活动”中,参加白云山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下:
例11:在市政府举办的“迎奥运登山活动”中,参加白云山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下:
(1)根据图①提供的信息补全图②;
(2)参加登山活动的12000余名市民中,哪个年龄段的人数最多?
(3)根据统计图提供的信息,谈谈自己的感想.(不超过30字)
3、方差,标准差与极差。方差:顾名思义是“差的平方”,因有多个“差的平方”,所以要求平均数,弄清是“数据与平均数差的平方的平均数”,标准差是它的算术平方根。 会用计算器计算标准差与方差。
例6:数据90,91,92,93的标准差是( )
(A) (B) (C) (D)
 例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
(A)甲的射击成绩较稳定 (B)乙的射击成绩较稳定
(C)甲、乙的射击成绩同样稳定 (D)甲、乙的射击成绩无法比较
例8:一个样本中,数据15和13各有4个,数据14有2个,求这个样本的平均数、方差、标准差和极差(标准差保留两个有效数字)
2、中位数,众数,平均数,加权平均数,注意区分这些概念。
相同点:都是为了描述一组数据的集中趋势的。
不同点:中位数--中间位置上的数据(当然要先按大小排列)
众数--出现的次数多的数据。
例3:某校篮球代表队中,5名队员的身高如下(单位:厘米):185,178,184,183,180,则这些队员的平均身高为( )
(A)183 (B)182 (C)181 (D)180
例4:已知一组数据为3,12,4,x,9,5,6,7,8的平均数为7,则x=
例5:某班第二组男生参加体育测试,引体向上成绩(单位:个)如下:
6 9 11 13 11 7 10 8 12
这组男生成绩的众数是____________,中位数是_________。
1、总体,个体,样本和样本容量。注意“考查对象”是所要研究的数据。
例1:为了了解某地区初一年级7000名学生的体重情况,从中抽取了500名学生的体重,就这个问题来说,下面说法中正确的是( )
(A)7000名学生是总体 (B)每个学生是个体
(C)500名学生是所抽取的一个样本 (D)样本容量是500
例2:某市今年有9068名初中毕业生参加升学考试,从中抽出300名考生的成绩进行分析。在这个问题中,总体是__________________________;个体是___ ________;样本是_______________________;样本容量是__________.
34、
解:如图,根据题意,有AB∥CD,PM⊥CD于N点,
交AB于M点,且AB=20m,
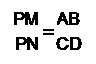 CD=50m, PM=25m,
CD=50m, PM=25m,
AB∥CD→△PAB∽△PCD→
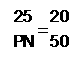
→ →PN=62.5→MN=37.5
33、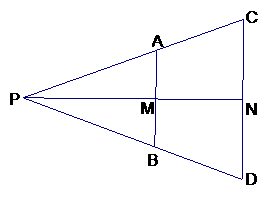 AD=AE→∠ADE=∠AED→∠ADB=∠AEC→△ABD≌△AEC→AB=AC
AD=AE→∠ADE=∠AED→∠ADB=∠AEC→△ABD≌△AEC→AB=AC
32、∠A=∠DBA→AD=BD→CD+BD=AC=18、△CDB的周长是28→BC=10
31、△BED≌△CFD→BE=CF
30、BE=CF、∠B=∠C、BD=DC→△BED≌△CFD→∠1=∠2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com