
题目列表(包括答案和解析)
|
坐标轴上点P(x,y) |
连线平行于坐标轴的点 |
点P(x,y)在各象限的坐标特点 |
象限角平分线上的点 |
|||||||
|
X轴 |
Y轴 |
原点 |
平行X轴 |
平行Y轴 |
第一象限 |
第二象限 |
第三象限 |
第四象限 |
第一、三象限 |
第二、四象限 |
|
(x,0) |
(0,y) |
(0,0) |
纵坐标相同 横坐标不同 |
横坐标相同 纵坐标不同 |
x>0 y>0 |
x<0 y>0 |
x<0 y<0 |
x>0 y<0 |
(m,m) |
(m,-m) |
关于x轴对称的点的横坐标相同,纵坐标互为相反数
关于y轴对称的点的纵坐标相同,横坐标互为相反数
关于原点对称的点的横坐标、纵坐标都互为相反数
平行于x轴(或横轴)的直线上的点的纵坐标相同;
平行于y轴(或纵轴)的直线上的点的横坐标相同。
(三)坐标方法的简单应用
1、用坐标表示地理位置;
2、用坐标表示平移。
(二)平面直角坐标系
1、历史:法国数学家笛卡儿最早引入坐标系,用代数方法研究几何图形 ;
2、构成坐标系的各种名称;
3、各种特殊点的坐标特点。
(一)有序数对:有顺序的两个数a与b组成的数对。
1、记作(a ,b);
2、注意:a、b的先后顺序对位置的影响。
㈠ 要使下列各式有意义,求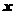 的取值范围:
的取值范围:
① 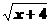 ②
②
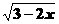 ③
③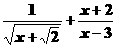 ④
④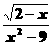
解题思路:二次根号有意义,被开方数应
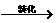 一元一次不等式
一元一次不等式
分式有意义,分母
㈡ 填空
适合不等式 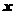 >
>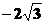 的负整数解是
的负整数解是
适合不等式 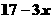 ≥
≥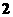 的正整数解是
的正整数解是
适合不等式 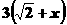 >
>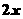 的最小负整数解是
的最小负整数解是
适合不等式 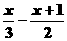 >
>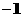 的非负整数解是
的非负整数解是
㈢ 当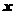 为何值时,
为何值时,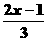 与
与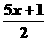 的差不大于
的差不大于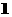 ?
?
㈣ 知识准备:
一元二次方程有两个相等的实根→ 0 →
0 →
一元二次方程有不两个相等的实根→ 0 →
0 →
一元二次方程没有实根→ 0 →
0 →
当 为何值时,关于
为何值时,关于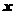 的方程
的方程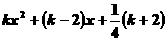 =
=
① 有两个相等的实根 ② 有两个不相等的实根
③ 没有实数根 ④ 有实数根
注意:在用判别式讨论含字母系数的一元二次方程的解时,在考虑前提条件: 二次项系数
⑴ 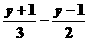 >
>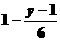 去分母 得
去分母 得
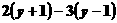 >
>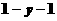
注意:去分母时,如果分子是一个多项式,应加
并且要注意不等式两边的每一项都乘以各分母的
⑵ 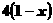 >
>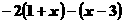 去括号
得
去括号
得
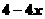 >
>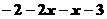
注意:去括号时,括号前面是负号,括号里各项都
⑶ 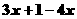 ≤
≤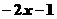 移项 得
移项 得
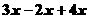 ≤
≤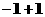
注意:移项时,所移的项要改变
⑷ 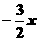 ≥
≥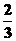 两边同除以
两边同除以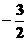 得
得
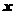 ≥
≥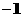
注意:两边同除以(或同乘以)一个负数时,不等号要改变
① ② ③ ④ ⑤
练习:解下列不等式
⑴ 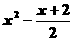 <
<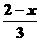 ⑵
⑵ 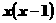 ≥
≥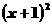
16、(10分)已知关于x、y的二元一次方程(a-1)x+(a+2)y+5-2a=0 ①
(1)当a=1时,得到方程②;当a=-2时,得到方程③,求由方程②③组成的方程组的解;
(2)将求得的解代入方程①的左边,会得到什么结论?由此得到什么结论?并验证你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com