6.现有1角、5角、1元的硬币各10枚,从中取出15枚,共值7元,三种硬币各取多少枚?

解:设1角、5角、1元的硬币分别取x、y、z枚.

得方程组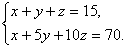

消去x得4y+9z=55.

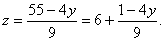
y=7.

或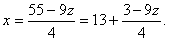

z=3.

∴x=5,y=7,z=3.

(答略.)

10.已知m是整数,且-60<m<-30,关于x、y的二元一次方程组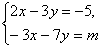有整数解,求m的值.

解:消去x,得m=6-11.5y,∴-60<6-11.5y<-30,y=4(x是分数,舍去)或y=5.这时,m=-50.

[练习]

黄先生对四个孩子说:"一定是你们当中的一个打破了玻璃,是谁?"

宝宝:"是可可."

可可:"不是我,是毛毛."

多多:"不是我."

毛毛:"可可撒谎."

若只有一个小孩说实话,问谁讲的是实话?玻璃是谁打破的

二元一次方程解应用题部分答案

9.一玩具工厂用于生产的全部劳力为450个工时,原料为400个单位.生产一个小熊要15个工时、20个单位的原料,售价为80元;生产一个小猫要使用10个工时,5个单位的原料,售价为45元.在劳力和原料的限制下合理安排生产小熊、小猫的个数,可以使小熊和小猫的总售价尽可能高.请你用你所学过的数学知识分析,总售价是否可能达到2200元?

8.某医疗器械厂生产甲、乙、丙三种医疗器械.生产每台各种器械所需的工时和产值如下表所示.又知道每周的总工时是168,总产值是111.2万元,若每周丙种器械生产252台,问其它两种器械每周分别生产多少台?

设每周生产甲种器械x台,你会列表分析这个问题吗?试一试.

想一想:根据列表分析,该如何列方程?

7.某运输公司拟用载重量分别为2.5吨和4吨的两种货车承运每件为120千克的健身器(不考虑体积)计420件.如果一共用两种汽车17辆,问需4吨的车几辆?

6.现有1角、5角、1元的硬币各10枚,从中取出15枚,共值7元,三种硬币各取多少枚?

5.在等式y=kx+b中,当x=0时,y=2;当x=3时,y=3.求当x=-3时,y的值.

4.若方程组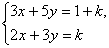的解满足x+y=2,求k的值.

3.某汽车刚开始行驶时, 油箱中有油90千克, 每小时的耗油量为6千克.

(1)求8小时后余油量;

(2)求余油量Q(千克)与行驶时间t(时)之间的关系式 ; 并在下边的直角坐标系中画出图象.

(3)若余油量Q是60(千克)时,行驶时间t是多少?你能从图象直接"看"出答案吗?

(4)你能从(2)中的关系式求出(3)的答案吗?

2.王平要从甲村走到乙村.如果他每小时走4千米,那么走到预定时间, 离乙村还有0.5千米;如果他每小时走5千米,那么比预定时间少用半小时就可到达乙村.求预定时间是多少小时,甲村到乙村的路程是多少千米.

解:设预定时间是x小时,甲村到乙村的路程是y千米.

根据"如果他每小时走4千米,那么走到预定时间, 离乙村还有0.5千米",

列方程:____________________________;

根据"如果他每小时走5千米,那么比预定时间少用半小时就可到达乙村",

列方程:_______________________.

(以下略.)