
题目列表(包括答案和解析)
1、2007-200.7´2+20.07´3-2.007´4 =______.
20. 有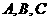 三个足球队,两两比赛一次,一共比赛了三场球,每个队的比赛结果累计填在下表内.根据表上的结果,你能不能写出三场球赛的具体比分?
三个足球队,两两比赛一次,一共比赛了三场球,每个队的比赛结果累计填在下表内.根据表上的结果,你能不能写出三场球赛的具体比分?
|
|
胜 |
负 |
平 |
入球 |
失球 |
 |
2 |
|
|
6 |
2 |
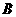 |
1 |
1 |
|
4 |
4 |
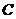 |
|
2 |
|
2 |
6 |
 失2球,如全是失于
失2球,如全是失于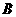 ,则
,则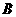 一共得4球,另2球是胜
一共得4球,另2球是胜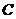 的,则
的,则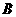 与
与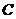 成2:2平,与知矛盾;如全是失于
成2:2平,与知矛盾;如全是失于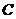 ,则
,则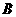 所得4球全是胜
所得4球全是胜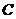 的,
的,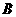 与
与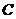 成4:0,
成4:0, 与
与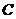 成2:2,矛盾.故
成2:2,矛盾.故 各失1球于
各失1球于 .
.
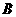 共入4球,另三球是胜
共入4球,另三球是胜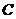 的,
的,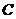 共入2球,另一球是胜
共入2球,另一球是胜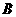 的,故
的,故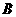 与
与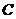 成3:1.
成3:1.
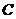 共失6球,另3球失于
共失6球,另3球失于 ,故
,故 与
与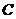 成3:1.
成3:1.
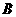 失4球,一球失于
失4球,一球失于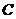 ,三球失于
,三球失于 ,故
,故 与
与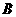 也成3:1.
也成3:1.
19.用1,4,5,6四个数,通过四则运算(允许用括号),组成一个算式,使算式的结果是24,那么这个算式是________.
4÷(1-5÷6).
18. 设有十个人各拿着一只提桶同时到水龙头前打水,设水龙头注满第一个人的桶需要1分钟,注满第二个人的桶需要2分钟,…….如此下去,当只有两个水龙头时,巧妙安排这十个人打水,使他们总的费时时间最少.这时间等于_________分钟.
[答案]125分钟
[解] 不难得知应先安排所需时间较短的人打水.
不妨假设为:
|
|
第一个水龙头 |
第二个水龙头 |
|
第一个 |
A |
F |
|
第二个 |
B |
G |
|
第三个 |
C |
H |
|
第四个 |
D |
I |
|
第五个 |
E |
J |
显然计算总时间时,A、F计算了5次,B、G计算了4次,C、H计算了3次,D、I计算了2次,E、J计算了1次.
那么A、F为1、2,B、G为3、4,C、H为5、6,D、I为7、8,E、J为9、10.
所以有最短时间为(1+2)×5+(3+4)×4+(5+6)×3+(7+8)×2+(9+10)×1=125分钟.
10.5
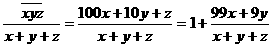 ,要使上式最小,显然
,要使上式最小,显然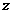 应该尽可能地大,于是
应该尽可能地大,于是 .从而原式=
.从而原式=
要使此式最小, 也应尽可能大,取
也应尽可能大,取 ,原式
,原式
 ,要使此式最小,
,要使此式最小, 应尽可能小,但
应尽可能小,但 ,故取
,故取
 .
.
故 的最小值是
的最小值是 .
.
17.
从0,1,2,3,4,5,6,7,8,9中取三个不同的数组成三位数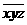 ,那么
,那么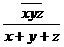 的最小值是_____.
的最小值是_____.
16. 某蓄水池有甲、丙两条进水管和乙、丁两条排水管.要灌满一池水,单开甲管需要3小时,单开丙管需要5小时;要排光一池水,单开乙管需要4小时,单开丁管需要6小时.现在池内有1/6池水,如果按甲、乙、丙、丁的顺序,循环开各水管,每次每管1小时.问多少时间后水开始溢出水池?
据已知条件,四管按甲乙丙丁顺序各开1小时,共开4小时,池内灌进的水是全池的 ;加上池内原来的水,池内有水
;加上池内原来的水,池内有水 .
.
再过四个4小时,即20小时后,池内有水 ,还需灌水
,还需灌水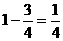 .此时可由甲管开
.此时可由甲管开 (小时).
(小时).
所以在 (小时)后,水开始溢出水池.
(小时)后,水开始溢出水池.
15. 有一个由9个小正方形组成的大正方形,将其中两个涂黑,有多少种不同的涂法?(如果几个涂法能够由旋转而重合,这几个涂法只能看作是一种,比如下面四个图,就只能算一种涂法.)




分类计算如下:当涂黑的两个方格占两角时,有2种涂法;当占两边时,也有2种涂法,当占一边一角时,有4种涂法;当占一角一中心时,有1种涂法;当占一边一中心时,也有1种涂法.
合计共有2+2+4+1+1=10(种)涂法.
8.
连结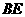 ,
, 的面积=
的面积=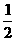 ×正方形
×正方形 的面积=
的面积=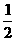 ×8×8=32;
×8×8=32;
 的面积=
的面积=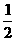 ×
× 的面积=16;
的面积=16;
 的面积=
的面积=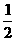 ×8×4=16;
×8×4=16;
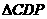 的面积=
的面积=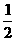 ×
× 的面积=
的面积=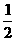 ×16=8.而
×16=8.而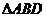 的面积=
的面积=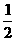 ×8×8=32.
×8×8=32.
故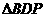 的面积=正方形
的面积=正方形 的面积-
的面积-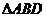 的面积-
的面积- 的面积-
的面积- 的面积=64-32-16-8=8(平方单位).
的面积=64-32-16-8=8(平方单位).
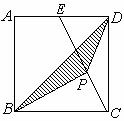
14.
如图,已知边长为8的正方形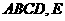 为
为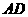 的中点,
的中点,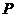 为
为 的中点,
的中点,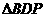 的面积________.
的面积________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com