27、(9分)某小区按照分期付款的形式福利购房，政府给予一定的补贴。小明家购得一套现价为120000元的房子，购房时首期(第一年)付款30000元。从第二年起，以后每年付房款为5000元与上一年剩余欠款利息的和，设剩余欠款的年利率为0.4%。

(1)若第x(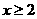)年小明家交付房款y元，求年付款y(元)与x(年)的函数关系式；

(2)将第三年、第十年应付房款填入下列表格中。

26、(8分)一次科技知识竞赛，两组同学成绩统计如下表：

请你根据所学过的统计知识，判断这次竞赛中成绩谁优谁劣，并说明理由。

25、(8分)浙江省移动公司开设有两种手机业务：①“全球通”：月租费为50元，市内通话费按0.4元/分计算；②“神州行”：不缴月租费，市内通话费按0.6元/分计算.若设一个月市内通话时间为x分，两种方式的通话费分别为和.则选择全球通合还是神州行合算？

24、(8分)已知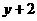与x成正比例，且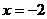时，。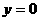

(1)y是x的一次函数吗？求y与x之间的函数关系式；

(2)求当x=1时y的值；

(3)求当y=3时x的值；

(4)求当-1<y≤2时x的取值范围。

23、(8分)解下列不等式(组)，并把解集表示在数轴上。

(1)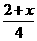≥　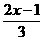　　　　 　　　　 (2)

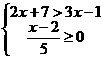
22、根据指令[s,A] (s≥0, 0⁰<A<180⁰), 机器人在平面上能完成下列动作: 先原地逆时针旋转角度A, 再朝其面对的方向沿直线行走距离s. 现机器人在直角坐标系的坐标原点, 且面对x轴正方向. (1) 若给机器人下了一个指令[4,60⁰]，则机器人应移动到点 ____; (2) 请你给机器人下一个指令 ____ , 使其移动到点 (-5,5).

21、在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点. 观察图4中每一个正方形(实线)四条边上的整点的个数，请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有_________个.

20、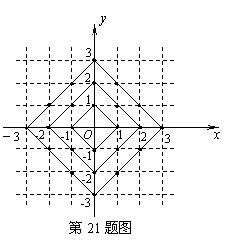如右图，△ABC边BC长是10，BC边上的高是6cm,D点在BC上运动，设BD长为x,请写出△ABD的面积y与x之间的函数关系式： 　__________，自变量x的取值范围是________，函数值y的取值范围是___________。

19、已知线段MN平行于x轴，且MN的长度为5，若M(2，-2)，那么线段MN上任意一点的坐标是__________.

18、已知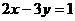，若把y看成x的函数，则可表示为　　　　　　 。