1.为了了解某市八年级学生某次数学统考情况。从参加考试的学生中抽查了500名学生的数学成绩，进行统计分析。在这个问题中。下列说法正确的是(　 )

A．总体是指该市参加统考的所有八年级考生　 B．个体是指500名学生中的每一名学生

C．样本是指这500名学生的统考数学成绩　　 D．样本是500名参加统考的学生

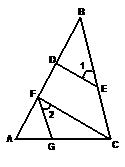
27、如图，已知：CF⊥AB于F，ED⊥AB于D，∠1＝∠2，

　　　　　 求证：FG∥BC

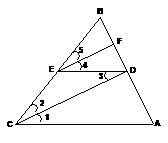
26、如图，已知：AC∥DE，DC∥EF，CD平分∠BCA

求证：EF平分∠BED.

25、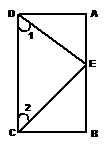如图：已知CB⊥AB，CE平分∠BCD，DE平分∠ADC，∠1+∠2＝90º

　　　 　 求证：AB∥CD

24、看图填空：

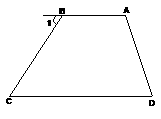
(1)　　 如下图左，∠A+∠D＝180º(已知)

∴　　　　 ∥　　　　 (　　　　　　　　 )

∴∠1＝　　　　　 　　(　　　　　　　　 )

∵∠1＝65º(已知)

∴∠C＝65º(　　　　　　　　　　　　　 )

(2)　　 如上图右，已知，∠ADC＝∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2，求证：∠A=∠C.

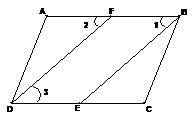证明：∵BE、DF分别平分∠ABC、∠ADC(已知)

∴ ∠1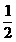＝∠ABC，∠3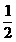＝∠ADC(　　　　 )

∵∠ABC＝∠ADC(已知)

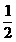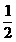∴∠ABC＝∠ADC(　　　　　 )

∴∠1＝∠3(　　　　　　　　　 )

∵∠1＝∠2(已知)

∴∠2＝∠3(　　　　　　　　　 )

∴(　　　 )∥(　　　 )(　　　　　　　　　　　 )

∴∠A+∠　　 ＝180º ，∠C+∠　　 ＝180º(　 　　　　　　)

∴∠A＝∠C(　　　　　　　　　 )

23、如图：

(1)　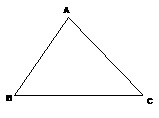　 画△ABC的外角∠BCD，再画∠BCD的平分线CE.

(2)　　 若∠A=∠B，请完成下面的证明：

已知：△ABC中，∠A=∠B，CE是外角∠BCD的平分线

求证：CE∥AB

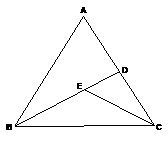
22、如图：∠A=65º ，∠ABD=∠DCE=30º，且CE平分∠ACB,求∠BEC.

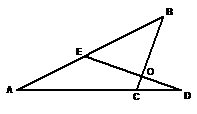
21、如图，BC⊥ED，垂足为O， ∠A=27º，∠D=20º，求∠ACB与∠B的度数.

20、如图，如果AB∥CD，则角α、β、γ之间的关系式为(　　 )

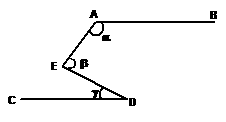
A、α+β+γ=360º　　　 　　　　

B、α－β+γ=180º　　　

C、α+β+γ=180º　　　 　　　　

D、α+β－γ=180º　

19、如上图右：AB∥CD，直线HE⊥MN交MN于E，∠1=130º，则∠2等于(　　 )

　A、50º　　　 B、40º　　　 C、30º　　　 D、60º