
题目列表(包括答案和解析)
2.3 一元二次方程的应用(1)同步练习
解题示范
例 某农户种植花生,老品种花生的每公顷产量为2 000千克,出油率为50%(即每100千克花生可加工成花生油50千克).现种植新品种花生后,每公顷收获的花生可加工成花生油1 320千克,其中花生出油率的增长率是每公顷产量增长率的一半,求新品种花生每公顷产量的增长率.
审题 本题已知老品种花生的每公顷产量与出油率、新品种花生每公顷可出油1 320千克,以及新品种花生的出油率的增长率与产量增长率的关系.未知新品种花生的每公顷产量及出油率.
方案 可设所求增长率为x,列表如下:
|
|
老品种 |
新品种 |
|
每公顷产量 |
2000千克 |
2000(1+x)千克 |
|
出油率 |
50% |
50%(1+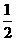 x) x) |
|
出油量 |
2000×50%千克 |
1320千克 |
从表中可寻找到相同对象的等量关系,从而可列出方程求解.
实施 设新品种花生每公顷产量的增长率为x,则新品种花生出油率的增长率为x.根据题意,得2 000(1+x)·50%(1+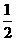 x)=1
320.
x)=1
320.
解得x1=0.2,x2=-3.2(不合题意,舍去).
∴ x=0.2=20%.
答:新品种花生公顷产量的增长率为20%.
反思 (1)当题中牵涉的量较多时,可通过列表的方式来分析、理解题意.
(2)列方程解应用题时,检验是必不可少的环节,我们需检验两个方面:一是检验未知数的值是否是原方程的解,二是未知数的值是否符合实际意义.
课时训练
8.在实数范围内,方程x2+1=0有解吗?x2-2x+2=0呢?
7.用一根长为24m的绳子围成面积为18m2的矩形,请问这个矩形的长与宽各是多少?
6.当x取何值时,代数式x2-3x+3的值等于7.
5.用配方法解下列方程:
(1)x2-2x=1; (2)x2+24=10x;
(3)x(x+2)=323; (4)x2+6x-91=0.
4.解方程:
(1)x2=121; (2)(x-3)2=16.
3.在横线上填上适当的数或式,使下列等式成立:
(1)x2+px+________=(x+_______)2;(2)x2+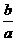 x+_________=(x+_______)2.
x+_________=(x+_______)2.
2.方程(x+1)2=9的解是_________.
1.填上适当的数,使下列等式成立:
(1)x2+2x+________=(x+______)2;(2)x2-6x+________=(x-______)2;
(3)t2-10t+________=(t-_______)2;(4)y2+_____y+121=(y+_______)2.
2.2 一元二次方程的解法(1)同步练习
解题示范
例 用配方法解下列一元二次方程:
(1)x2+12x=9 964; (2)9x2-12x=1.
审题 本题要求用配方法解一元二次方程,因此方程的左边应先化成(ax+b)2的形式.
方案 对于第(1)小题,配方较为容易,只需两边都加上36即可.对于第(2)小题,联想公式(a+b)2=a2+2ab+b2,应在方程两边都加上4,才能把左边的式子化成(ax+b)的形式.
实施 (1)x2+12x=9 964.
两边都加上36,得x2+12x+36=9 964+36.
即(x+6)2=10 000.
∴ x+6=100,或x+6=-100.
解得x1=94,x2=-106.
(2)9x2-12x=1.
两边都加上4,得9x2-12x+4=1+4,即(3x-2)2=5.
∴ 3x-2=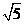 ,或3x-2=-
,或3x-2=-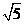 .
.
解得 x1=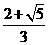 ,x2=
,x2=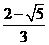 .
.
反思 对二次项系数为1的一元二次方程进行配方,应在方程两边都加上一次项系数一半的平方.
课时训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com