
题目列表(包括答案和解析)
6、如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于( )
(A)8 (B)14 (C)8或14 (D)-8或-14
5、若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(-1,0),则S=a+b+c的变化范围是 ( )
(A) 0<S<2 (B) S>1 (C) 1<S<2 (D)-1<S<1
4、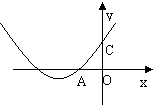 抛物线y=ax2+bx+c的图象如图,OA=OC,则 ( )
抛物线y=ax2+bx+c的图象如图,OA=OC,则 ( )
(A) ac+1=b (B) ab+1=c (C)bc+1=a (D)以上都不是
3、已知二次函数y=ax2+bx的图象经过点A(-1,1),则ab有 ( )
(A)最小值0
(B)最大值 1 (C)最大值2 (D)有最小值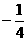
2、下列四个函数中,y的值随着x值的增大而减小的是( )
(A)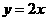 (B)
(B)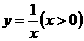 (C)
(C)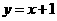 (D)
(D)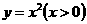
1、二次函数y=x2-(12-k)x+12,当x>1时,y随着x的增大而增大,当x<1时,y随着x的增大而减小,则k的值应取( )
(A)12 (B)11 (C)10 (D)9
30.已知抛物线y=x2-kx+k+4与x轴正半轴从左到右交于点A(x1,0)和B(x2,0)不同的两点,与Y轴交于G,H为OG中点,且x12+x22=40
(1)求此抛物线的解析式及顶点C坐标;
(2)若抛物线的对称轴交X轴于D,E为DC中点;过A、B、E三点作圆,过H的直线与该圆相切于P,求直线HP的方程;
(3)设F(m,n)为抛物线上一点,若解析式为y=a的直线MN与抛物线交点为M、N,是否存在实数a,使得△MNF为等边三角形,若存在,求出a的值;若不存在,请说明理由。
(第30题)
29.如图:⊙O与直线PC相切于点C,直径AB∥PC,PA交⊙O于D,BP交⊙O于E,DE交PC于F
(1)求证:PF2=EF·FD
(2)当tan∠APB=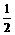 ,tan∠ABE=
,tan∠ABE=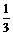 ,AP=
,AP=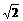 时,求PF的长。
时,求PF的长。
(3)在(2)条件下,连接BD,判断△ADB是什么三角形?并证明你的结论。
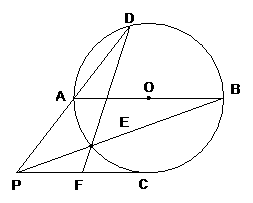
(第29题)
28.甲、乙两同学开展“投球进筐”比赛,双方约定:① 比赛分6局进行,每局在指定区域内将球投向筐中,只要投进一次后该局便结束;② 若一次未进可再投第二次,以此类推,但每局最多只能投8次,若8次投球都未进,该局也结束;③ 计分规则如下:a. 得分为正数或0;b. 若8次都未投进,该局得分为0;c. 投球次数越多,得分越低;d. 6局比赛的总得分高者获胜 .
(1) 设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进,请你按上述约定,用公式、表格或语言叙述等方式,为甲、乙两位同学制定一个把n换算为得分M的计分方案;
(2) 若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数,“×”表示该局比赛8次投球都未进):
|
|
第一局 |
第二局 |
第三局 |
第四局 |
第五局 |
第六局 |
|
甲 |
5 |
× |
4 |
8 |
1 |
3 |
|
乙 |
8 |
2 |
4 |
2 |
6 |
× |
根据上述计分规则和你制定的计分方案,确定两人谁在这次比赛中获胜.

27.幼儿园王老师有240颗糖,计划平均分给每一位小朋友,恰好分完。分糖时,明明由于有蛀牙不能吃糖,于是王老师把240颗糖平均分给其他每一位小朋友,恰好分完,且每人分得的糖比王老师计划的要多1颗。求幼儿园小朋友的人数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com