12.解：如图建立平面直角坐标系，由题意

可设A、B两人速度分别为3v千米/小时 ，

v千米/小时，再设出发x₀小时，在点P改变

方向，又经过y₀小时，在点Q处与B相遇.

则P、Q两点坐标为(3vx₀, 0)，(0,vx₀+vy₀).

由|OP|²+|OQ|²=|PQ|²知，

(3vx₀)²+(vx₀+vy₀)²=(3vy₀)²,

即.

……①

将①代入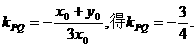

又已知PQ与圆O相切，直线PQ在y轴上的截距就是两个相遇的位置.

设直线相切，

则有

答：A、B相遇点在离村中心正北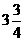千米处

C组：

11.解：(Ⅰ)证明：直线l：可化为

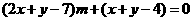
由于m∈R，则，解得，

∴直线l经过定点A(3，1).

又∵　圆C的圆心坐标为(1，2)，且│AC│＝＜5(半径)， ∴　点A在圆C内，

从而不论m为何值，直线l恒与圆C相交于两点． (Ⅱ)解：要使弦长最小时，必须l⊥AC， 由k_BC＝－，知k₁＝2，m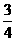＝－． 所以直线l的方程为2x－y－5＝0．

10.解：圆(x－2)²+(y－2)²＝1关于x轴的对称方程是(x－2)²+(y+2)²＝1.

设l方程为y－3＝k(x+3)，由于对称圆心(2，－2)到l距离为圆的半径1，从而可得k₁＝－，k₂＝－．故所求l的方程是3x+4y－3＝0或4x+3y+3＝0.

6. (x+1)²+(y-1)²=13 　 7.　 (－1，2)　 8.　 2　　　 9　 －1＜k≤1或k=－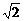

12.解：(1)已知圆C：的圆心为C(1，0)，因直线过点P、C，所以直线l的斜率为2，

　　　 直线l的方程为y=2(x-1),即　 2x-y-2=0.

(2)当弦AB被点P平分时，l⊥PC,　 直线l的方程为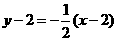, 即　 x+2y-6=0

(3)当直线l的倾斜角为45º时，斜率为1，直线l的方程为y-2=x-2 ,即 x-y=0

圆心C到直线l的距离为，圆的半径为3，

弦AB的长为.

B组：

11.解：设点M的坐标为(x，y)，由于，则，

整理得：　 即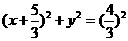 　

这就是点M的轨迹方程.图形为以(－，0)为圆心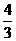，为半径的圆.

10.解：解：设所求圆的方程为，则

，解得或．

所以，所求圆的方程为，或．

6. 8　　　 7. x=-1或3x-4y+27=0　　 8.. 　　9.　 (x-2)²+(y+3)²=5

4、如图，在平面斜坐标系xOy中，∠xOy=60°，平面上任一点P关于斜坐标系的斜坐标是这样定义的：若=xe₁+ye₂(其中e₁、e₂分别为与x轴、y轴同方向的单位向量)，则P点斜坐标为(x，y).

(1)若P点斜坐标为(2，－2)，求P到O的距离|PO|；

(2)求以O为圆心，1为半径的圆在斜坐标系xOy中的方程.

答案与提示

A组：

3、.圆内有一点P(-1,2),AB过点P,

①　　 若弦长，求直线AB的倾斜角；

②若圆上恰有三点到直线AB的距离等于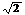，求直线AB的方程.