
题目列表(包括答案和解析)
(12分)已知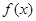 是二次函数,不等式
是二次函数,不等式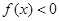 的解集是
的解集是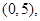 且
且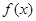 在区间
在区间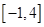 上的最大值是12.
上的最大值是12.
(1)求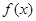 的解析式;
的解析式;
(2)是否存在实数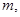 使得方程
使得方程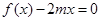 在区间
在区间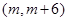 内有且只有两个不等的
内有且只有两个不等的
实数根?若存在,求出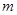 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且 在区间
在区间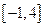 上的最大值是12.
上的最大值是12.  的解析式;
的解析式; 使得方程
使得方程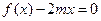 在区间
在区间 内有且只有两个不等的
内有且只有两个不等的 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.在 中,
中,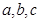 ,分别是角
,分别是角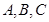 所对边的长,
所对边的长,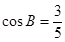 ,且
,且
(1)求 的面积;
的面积;
(2)若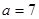 ,求角C.
,求角C.
【解析】第一问中,由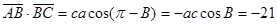 又∵
又∵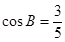 ∴
∴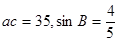 ∴
∴ 的面积为
的面积为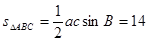
第二问中,∵a =7 ∴c=5由余弦定理得: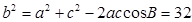 得到b的值,然后又由余弦定理得:
得到b的值,然后又由余弦定理得: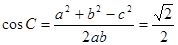
又C为内角 ∴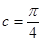
解:(1)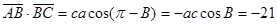 ………………2分
………………2分
又∵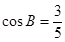 ∴
∴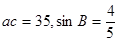 ……………………4分
……………………4分
∴ 的面积为
的面积为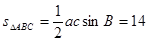 ……………………6分
……………………6分
(2)∵a =7 ∴c=5 ……………………7分
由余弦定理得: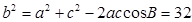
∴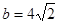 ……………………9分
……………………9分
又由余弦定理得: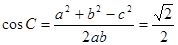
又C为内角 ∴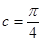 ……………………12分
……………………12分
另解:由正弦定理得: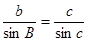 ∴
∴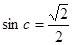 又
又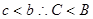 ∴
∴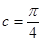
(1)若由一个2×2列联表中的数据计算得K2=4.013,那么有________的把握认为两个变量有关系;
(2)某企业为了更好地了解设备改造前后与生产合格品的关系,随机抽取了一些产品情况,具体数据如下表:

为了判断产品是否合格与设备改造是否有关系,根据表中的数据,得K2的观测值k=![]() ≈12.38.因为12.38>10.828,所以判定产品是否合格与设备改造有关系,那么这种判断出错的可能性为________.
≈12.38.因为12.38>10.828,所以判定产品是否合格与设备改造有关系,那么这种判断出错的可能性为________.
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com