题目列表(包括答案和解析)
| x2 |
| 16 |
| y2 |
| 12 |
| x2 |
| 16 |
| y2 |
| 12 |
| |CD| |
| |AB| |
| 2 |
| F2A |
| F2B |
椭圆中心在原点，且经过定点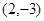
，其一个焦点与抛物线
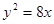的焦点重合，则该椭圆的方程为
抛物线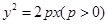
的焦点与椭圆
的一个焦点重合，且抛物线与椭圆的一个交点为
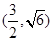，（1）求抛物线与椭圆的方程，（2）若过点
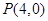的直线与抛物线交于点
，求
的最小值
椭圆
的方程为
，离心率为
，且短轴一端点和两焦点构成的三角形面积为1，抛物线
的方程为
，抛物线的焦点F与椭圆的一个顶点重合.
（1）求椭圆和抛物线的方程；
（2）过点F的直线交抛物线于不同两点A,B，交y轴于点N，已知
的值.
（3）直线
交椭圆于不同两点P,Q，P,Q在x轴上的射影分别为P′,Q′，满足
(O为原点)，若点S满足
，判定点S是否在椭圆上，并说明理由.
一、选择题（4′×10=40分）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
D
C
A
A
B
A
三、填空题（4′×4=16分）
11．
12．
13．
14．
三、解答题（共44分）
15．①解：原不等式可化为：
………………………2′
作根轴图：
………………………4′
可得原不等式的解集为：
………………………6′
②解：直线
的斜率
………………………2′
∵直线
与该直线垂直
∴
………………………4′
则的方程为：
………………………5′
即
为所求………………………6′
16．解：∵
∴
，
且
………………………1′
于是
………………………3′
………………………4′
………………………5′
当且仅当：
即
………………………6′
时，
………………………7′
17．解：将
代入
中变形整理得：
………………………2′
首先
且
………………………3′
设
由题意得：
解得：
或
（舍去）………………………5′
由弦长公式得：
………………………7′
18．解①设双曲线的实半轴，虚半轴分别为
，
由题得：
∴
………………………1′
于是可设双曲线方程为：
………………………2′
将点
代入可得：
，
∴该双曲线的方程为：
………………………4′
②直线方程可化为：
，
则它所过定点
代入双曲线方程：得：
∴
………………………6′
又由得
，
∴
，
或
，
…………7′
∴
∴
……………………8′
19．解：①设中心
关于的对称点为
，
则
解得：
∴
，又点
在左准线
上，
轴
∴的方程为：
……………………4′
②设
、
、
、
∵
、
、
成等差数列，
∴
，
即：
亦：
∴
……………………6′
∴
由
得
……………………8′
∴
， ∴
又由
代入上式得：
∴
，
∴
……………………9′
∴
，
，
∴椭圆的方程为：
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com