
题目列表(包括答案和解析)
0<a≤![]() 是函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数的
是函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数的
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
若函数f(x)=ax2-x-1在区间(0,2)内是单调函数,则实数a的取值范围是( )
A.0<a≤![]() B.a≤
B.a≤![]()
C.a≤0或a≥![]() D.a≤0
D.a≤0
函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,则实数a的取值范围是
A.![]() <a<1或a>1
<a<1或a>1
B.a>1
C.![]() <a<1
<a<1
D.0<a<![]()
设函数f(x)=ax2+2bx+c(a<b<c),m是方程f(x)=-a的实根,且f(1)=0.
(1)证明:-3<![]() ≤-1且b≤0;
≤-1且b≤0;
(2)判断f(m-4)的符号,并加以证明.
已知函数f(x)=ax2+bx+c的图象如图所示,则b的取值范围是
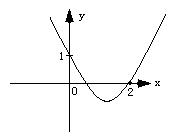
[ ]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com