
题目列表(包括答案和解析)
设函数
(1)当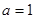 时,求曲线
时,求曲线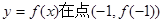 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数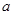 的取值范围.
的取值范围.
【解析】(1)中,先利用 ,表示出点
,表示出点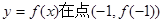 的斜率值
的斜率值 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当 ,再令
,再令 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当 ……2分
……2分
 ∴
∴
即 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令 ………………6分
………………6分
∴ 递减,在(3,+
递减,在(3,+ )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)
①若 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数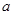 的取值范围是
的取值范围是
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
(本题满分16分,第(1)小题8分,第(2)小题8分)
己知双曲线的中心在原点,右顶点为![]()
![]() (1,0),点
(1,0),点![]() 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点![]() (
(![]() ,0)到直线
,0)到直线![]() 的距离为1.
的距离为1.
(1)若直线![]() 的斜率为
的斜率为![]() 且有
且有 ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]()
![]() 的内心恰好是点
的内心恰好是点![]() ,求此双曲线的方程.
,求此双曲线的方程.
(本题16分,其中第(1)小题8分,第(2)小题8分)
已知椭圆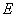 的方程为
的方程为 ,长轴是短轴的2倍,且椭圆
,长轴是短轴的2倍,且椭圆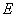 过点
过点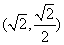 ;斜率为
;斜率为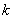 的直线
的直线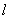 过点
过点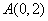 ,
,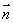 为直线
为直线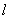 的一个法向量,坐标平面上的点
的一个法向量,坐标平面上的点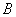 满足条件
满足条件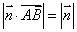 .
.
(1)写出椭圆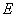 方程,并求点
方程,并求点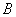 到直线
到直线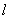 的距离;
的距离;
(2)若椭圆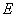 上恰好存在3个这样的点
上恰好存在3个这样的点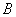 ,求
,求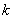 的值.
的值.
 (2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分
(2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分| π | 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com