
题目列表(包括答案和解析)
如图所示,在正三角形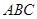 中,
中,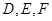 分别为各边的中点,
分别为各边的中点,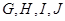 分别为
分别为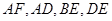 的中点,将
的中点,将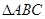 沿
沿
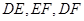 折成三棱锥后,
折成三棱锥后,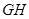 与
与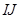 所成的角的度数为____。
所成的角的度数为____。
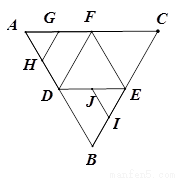
三个12cm×12cm的正方形纸片都被连接两条邻边的中点的直线分成两片,如图a所示,把所得的六片纸片粘在一个正六边形的外面,如图b所示,然后折成多面体,如图c所示,则此多面体的体积是
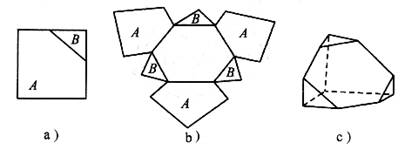
A.216cm3 B.648cm3 C.864cm3 D.1728cm3
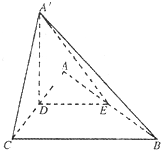 (2013•郑州一模)如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE.
(2013•郑州一模)如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE. (2013•郑州一模)如图,△ABC是等腰直角三角形∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE
(2013•郑州一模)如图,△ABC是等腰直角三角形∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE锐角△ABC中,![]() ,分别以BC,CA,AB边上的高AD,BE,CF为折线,将三角形折成平面角均为
,分别以BC,CA,AB边上的高AD,BE,CF为折线,将三角形折成平面角均为![]() 的二面角,记折叠后的四面体ABCD,ABCE,ABCF体积方便为
的二面角,记折叠后的四面体ABCD,ABCE,ABCF体积方便为![]() ,则下面结论正确的是 ( )
,则下面结论正确的是 ( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 大小不能确定
大小不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com