题目列表(包括答案和解析)
设f（x）是定义在[a，b]上的函数，用分点T：a=x0＜x1＜…＜x i﹣1＜xi＜…xn=b
将区间[a，b]任意划分成n个小区间，
如果存在一个常数M＞0，使得
和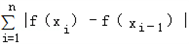
≤M（i=1，2，…，n）恒成立，
则称f（x）为[a，b]上的有界变差函数．
（1）函数f（x）=x2在[0，1]上是否为有界变差函数？请说明理由；
（2）设函数f（x）是[a，b]上的单调递减函数，证明：f（x）为[a，b]上的有界变差函数；
（3）若定义在[a，b]上的函数f（x）满足：存在常数k，使得对于任意的x1、x2∈[a，b]时，|f（x1）﹣f（x2）|≤k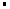
|x1﹣x2|．证明：f（x）为[a，b]上的有界变差函数．
①若存在常数M，使得对任意x∈R有f(x)≤M,则M是函数f(x)的最大值；
②若存在x0∈R,使得对任意x∈R且x≠x0有f(x)＜f(x0)，则f(x0)是函数f(x)的最大值；
③若存在x0∈R，使得对任意x∈R,有f(x)≤f(x0)，则f(x0)是函数f(x)的最大值.
这些命题中，真命题的个数是（ ）
A.0 B.1 C.2 D.3
设函数f(x)的定义域为R，若存在与x无关的正常数M，使
对一切实数x均成立，则称f(x)为“有界泛函”，给出以下函数：
|
④
其中是“有界泛函”的个数为
A．0 B．1 C．2 D．3
设函数f(x)的定义域为R，若存在常数M＞0使|f(x)|≤M|x|对一切实数x均成立，
则称函数f(x)为F函数．现给出下列函数①f(x)＝x2，②f(x)＝
，③f(x)＝x(1－2x)，④f(x)是定义在实数集R上的奇函数，且对一切x1x2均有|f(x1)－f(x2)|≤2|x1－x2|．其中是F函数的序号为
A．①②③
B．②④
C．②③
D．③④
设函数
f(x)＝a2x2(a＞0)，g(x)＝blnx．(1)
将函数y＝f(x)图象向右平移一个单位即可得到函数y＝φ(x)的图象，试写出y＝φ(x)的解析式及值域；(2)
关于x的不等式(x－1)2＞f(x)的解集中的整数恰有3个，求实数a的取值范围；(3)
对于函数f(x)与g(x)定义域上的任意实数x，若存在常数k，m，使得f(x)≥kx＋m和g(x)≤kx＋m都成立，则称直线y＝kx＋m为函数f(x)与g(x)的“分界线”．设
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com