练习册

  • 练习册
  • 试题
    25 【查看更多】

     

    题目列表(包括答案和解析)

    25②（供选用《选修3-l》物理课教材的学生做）
    如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E，场区宽度为L．在紧靠电场的右侧空间分布着方向垂直于纸面的两个匀强磁场，磁感应强度均为B，两磁场的方向相反、分界面与电场边界平行，且右边磁场范围足够大．一质量为m、电荷量为q的带正电的粒子从A点由静止释放后，在电场和磁场存在的空间进行周期性的运动．已知电场的右边界到两磁场分界面间的距离是带电粒子在磁场中运动的轨道半径的
    		3
    2
    倍，粒子重力不计．求：
    （1）粒子经电场加速后，进入磁场的速度大小；
    （2）粒子在磁场中运动的轨道半径；
    （3）粒子从A点出发到第一次返回A点的时间．

    查看答案和解析>>

    (25分)如图所示，两个金属轮A1、A2，可绕通过各自中心并与轮面垂直的固定的光滑金属轴O1和O2转动，O1和O2相互平行，水平放置.每个金属轮由四根金属辐条和金属环组成，A1轮的辐条长为a1、电阻为R1，A2轮的辐条长为a2、电阻为R2，连接辐条的金属环的宽度与电阻都可以忽略.半径为a0的绝缘圆盘D与A1同轴且固连在一起.一轻细绳的一端固定在D边缘上的某点，绳在D上绕足够匝数后，悬挂一质量为m的重物P.当P下落时，通过细绳带动D和A1绕O1轴转动.转动过程中，A1、A2保持接触，无相对滑动；两轮与各自细轴之间保持良好的电接触；两细轴通过导线与一阻值为R的电阻相连.除R和A1、A2两轮中辐条的电阻外，所有金属的电阻都不计.整个装置处在磁感应强度为B的匀强磁场中，磁场方向与转轴平行.现将P释放，试求P匀速下落时的速度.

    查看答案和解析>>

    (25分)图示为一固定不动的绝缘的圆筒形容器的横截面，其半径为R，圆筒的轴线在O处.圆筒内有匀强磁场，磁场方向与圆筒的轴线平行，磁感应强度为B.筒壁的H处开有小孔，整个装置处在真空中.现有一质量为m、电荷量为q的带电粒子P以某一初速度沿筒的半径方向从小孔射入圆筒，经与筒壁碰撞后又从小孔射出圆筒.设：筒壁是光滑的，P与筒壁碰撞是弹性的，P与筒壁碰撞时其电荷量是不变的.若要使P与筒壁碰撞的次数最少，问：

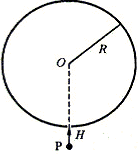
    1.P的速率应为多少？

    2.P从进入圆筒到射出圆筒经历的时间为多少？

    查看答案和解析>>

    (25分)图中正方形ABCD是水平放置的固定梁的横截面，AB是水平的，截面的边长都是l.一根长为2l的柔软的轻细绳，一端固定在A点，另一端系一质量为m的小球，初始时，手持小球，将绳拉直，绕过B点使小球处于C点.现给小球一竖直向下的初速度v0，使小球与CB边无接触地向下运动，当，分别取下列两值时，小球将打到梁上的何处？

    1.

    2.

    设绳的伸长量可不计而且绳是非弹性的.

    查看答案和解析>>

    (25分)从赤道上的C点发射洲际导弹，使之精确地击中北极点N，要求发射所用的能量最少.假定地球是一质量均匀分布的半径为R的球体，R=6400km.已知质量为m的物体在地球引力作用下作椭圆运动时，其能量E与椭圆半长轴a的关系为式中M为地球质量，G为引力常量.

    　　

    1.假定地球没有自转，求最小发射速度的大小和方向(用速度方向与从地心O到发射点C的连线之间的夹角表示).

    2.若考虑地球的自转，则最小发射速度的大小为多少？

    3.试导出。

    查看答案和解析>>

    一、全题共计15分,每小题3分:                1.D     2.B    3.A    4.C    5.D

    二、全题共计16分,每小题4分，漏选的得２分:    6.AD    7.BD    8. ABD     9.BD

    三、全题共计42分

    10.（8分）⑴20.30    ⑵①S1/2T；② 9.71～9.73  ③阻力作用  (每空2分)

    11．（10分）第⑶问4分，其中作图2分；其余每小问2分．⑶半导体材料　⑷4.0 、  0.40

     

     

            

     

     

     

     

     

    12．(12分) ⑴D （3分）   ⑵AC（3分）

    ⑶这种解法不对．

    错在没有考虑重力加速度与高度有关(2分)

    正确解答：卫星绕地球做匀速圆周运动，万有引力提供向心力，根据牛顿第二定律有

    G=mA ③    G=mB ④     由③④式，得 （4分）

    13A.(12分) ⑴不变（2分）  50（2分）  ⑵a→b（2分） 增加（2分） ⑶（4分）

    13B.(12分) ⑴C（3分 ） ⑵60°（2分） 偏右（2分）  ⑶（2分）　0.25s（3分）

    13C.(12分)    ⑴质子 、α 、氮     ⑵ mv2/4      ⑶a 、  5×1013    （每空2分）

    四、全题共计47分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位

    14.(15分) 解：⑴A→C过程，由动能定理得： ………… （3分）

    △R= R (1－cos37°)………………  （1分） ∴ vc=14m/s ……………………  （1分）

      ⑵在C点，由牛顿第二定律有： ……（2分）

    ∴ Fc=3936N …………………………………………………………………………（ 2分）

        由牛顿第三定律知，运动员在C点时轨道受到的压力大小为3936N. …………… （1分）

    ⑶设在空中飞行时间为t，则有：tan37°= 　…………………　　　　（ 3分）

     ∴t = 2.5s   (t =－0.4s舍去)……………………………………………………（ 2分）

     

     

     

    15.(16分) 解：⑴垂直AB边进入磁场，由几何知识得：粒子离开电场时偏转角为30°

    ∵………（2分）    

    ………  （1分）     ∴………（2分）

    由几何关系得：    在磁场中运动半径……（2分）

    ∴        ……………………………（2分）

    ∴……………（1分 ） 方向垂直纸面向里……………………（1分）

    ⑶当粒子刚好与BC边相切时，磁感应强度最小，由几何知识知粒子的运动半径r2为：

         ………（ 2分 ）   ………1分   ∴……… 1分

    即：磁感应强度的最小值为………（1分）

    16．(16分)

    解：⑴据能量守恒，得  △E = mv02 -m（）2= mv02-----------（3分）

    ⑵在底端，设棒上电流为I，加速度为a，由牛顿第二定律，则：

    （mgsinθ+BIL）=ma1--------------------------（1分）

    由欧姆定律，得I=---------------（1分）    E=BLv0---------------------（1分）

    由上述三式，得a1 =  gsinθ + ---------------------（1分）

    ∵棒到达底端前已经做匀速运动∴mgsinθ= ------------------------------（1分）

    代入，得a1 = 5gsinθ-----------------------------------------（2分）

    （3）选沿斜面向上为正方向，上升过程中的加速度，上升到最高点的路程为S，

    a = －（gsinθ + ）-----------------------（1分）

    取一极短时间△t，速度微小变化为△v，由△v = a△t，得

    △     v = －（ gsinθ△t+B2L2v△t/mR）-----------（1分）

    其中，v△t = △s--------------------------（1分）

    在上升的全过程中

    ∑△v = －（gsinθ∑△t+B2L2∑△s/mR）

    即          0-v0= －（t0gsinθ+B2L2S/mR）-------------（1分）

    ∵H=S?sinθ       且gsinθ= -------------------（1分）

    ∴  H =（v02-gv0t0sinθ）/4g-----------------（1分）

     

     

     

     


    同步练习册答案