
题目列表(包括答案和解析)
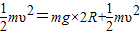 v=
v=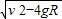 =1米/秒
=1米/秒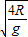 =
=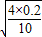 秒=0.283秒
秒=0.283秒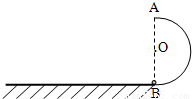
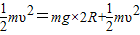 v=
v= =1米/秒
=1米/秒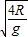 =
= 秒=0.283秒
秒=0.283秒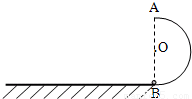
 如图所示,竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上,水平地面与轨道相切于B点.小球以υ0=3m/s的速度从最低点B进入轨道,关于小球落地点和轨道最低点B的距离,某同学做如下计算:
如图所示,竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上,水平地面与轨道相切于B点.小球以υ0=3m/s的速度从最低点B进入轨道,关于小球落地点和轨道最低点B的距离,某同学做如下计算:| 1 |
| 2 |
| 1 |
| 2 |
|
|
|
质量为m1的登月舱连接在质量为m2的轨道舱上一起绕月球作圆周运动,其轨道半径是月球半径Rm的3倍。某一时刻,登月舱与轨道舱分离,轨道舱仍在原轨轨道上运动,登月舱作一瞬间减速后,沿图示椭圆轨道登上月球表面,在月球表面逗留一段时间后,快速启动发动机,使登月舱具有一合适的初速度,使之沿原椭圆轨道回到脱离点与轨道舱实现对接。由开普勒第三定律可知,以太阳为焦点作椭圆轨道运行的所有行星,其椭圆轨道半长轴的立方与周期的平方之比是一个常量。另,设椭圆的半长轴为a,行星质量为m,太阳质量为M0,则行星的总能量为![]() 。行星在椭圆轨道上运行时,行星的机械能守恒,当它距太阳的距离为r时,它的引力势能为
。行星在椭圆轨道上运行时,行星的机械能守恒,当它距太阳的距离为r时,它的引力势能为![]() 。G为引力恒量。设月球质量为M,不计地球及其它天体对登月舱和轨道舱的作用力。求:
。G为引力恒量。设月球质量为M,不计地球及其它天体对登月舱和轨道舱的作用力。求:
(1)登月舱减速时,发动机做了多少功?
(2)登月舱在月球表面可逗留多长时间?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com