
题目列表(包括答案和解析)
(12分)一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为![]() ,出现“×”的概率为
,出现“×”的概率为![]() .若第
.若第![]() 次出现“○”,则a
次出现“○”,则a![]() =1;出现“×”,则a
=1;出现“×”,则a![]() =
=![]() .令S
.令S![]() =a
=a![]() +a
+a![]() +…+a
+…+a![]()
![]() .
.
(1)当![]() 时,求S
时,求S![]()
![]() 2的概率;
2的概率;
(12分)某校举行一次乒乓球比赛,在单打比赛中,甲、乙两名同学进入决赛,根据以往经验,单局比赛甲胜乙的概率为![]() ,本场比赛采用五局三胜制,即先胜三局者获胜,比赛结束.设各局比赛相互间没有影响.
,本场比赛采用五局三胜制,即先胜三局者获胜,比赛结束.设各局比赛相互间没有影响.
(1)试求本场比赛中甲胜两局最终乙获胜的事件![]() 的概率;
的概率;
(2)令![]() 为本场比赛的局数,求
为本场比赛的局数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
(满分13分)已知函数![]()
(1)求![]() 的单调区间;
的单调区间;
(2)记![]() 在区间
在区间![]()
![]() 上的最小值为
上的最小值为![]() 令
令![]() ;
;
①如果对一切n,不等式![]() 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
②求证: ![]() 。
。
.(12分)
设等差数列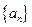 的前
的前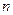 项和为
项和为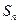 ,已知
,已知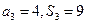 。
。
(1)求数列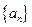 的通项公式;
的通项公式;
(2)令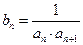 ,求数列
,求数列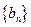 的前10项和。
的前10项和。
(14分)设函数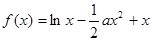
(1)当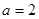 时,求
时,求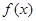 的最大值;
的最大值;
(2)令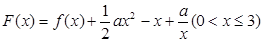 ,以其图象上任意一点
,以其图象上任意一点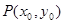 为切点的切线的斜率
为切点的切线的斜率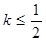 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当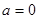 时,方程
时,方程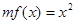 有唯一实数解,求正数
有唯一实数解,求正数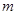 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com