
题目列表(包括答案和解析)
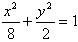 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0),
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0), 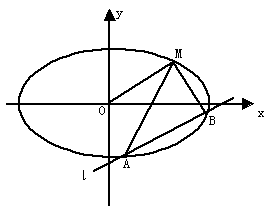
如图,已知离心率为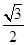 的椭圆
的椭圆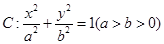 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
(1)求椭圆C的方程。
(2)证明:直线MA、MB与x轴围成一个等腰三角形。
(本小题满分12分)
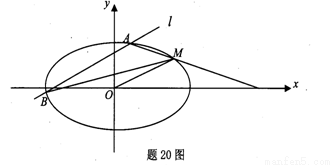
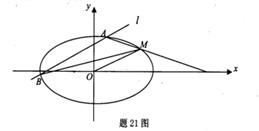
如题21图,已知离心率为 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
(1)求椭圆C的方程。
(2)证明:直线MA、MB与x轴围成一个等腰三角形。

(本小题满分12分)
如题21图,已知离心率为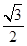 的椭圆
的椭圆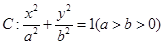 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线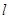 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
(1)求 面积的最大值;
面积的最大值;
(2)证明:直线MA、MB与x轴围成一个等腰三角形。
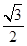 的椭圆
的椭圆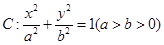 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线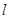 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;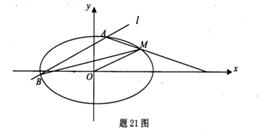
一、选择题:本大题共12小题,每小题5分,共60分。
ABBD DBBA BCBA
二、填空题:本大题共4小题,每小题4分,共16分。
13.2 14.3 15. 16.①③
16.①③
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.解:(I) ………2分
………2分
依题意函数
所以 …………4分
…………4分

(II)

18.解:(I)由题意得:上年度的利润的 万元;
万元;
本年度每辆车的投入成本为 万元;
万元;
本年度每辆车的出厂价为 万元;
万元;
本年度年销售量为 ………………2分
………………2分
因此本年度的利润为

(II)本年度的利润为

………………7分
则
由 (舍去)。 …………9分
(舍去)。 …………9分
|